Contents
【問題】
【難易度】★★★★☆(やや難しい)
図に示すような,相電圧\( \ E \ \mathrm {[V]} \ \),周波数\( \ f \ \mathrm {[Hz]} \ \)の対称三相\( \ 3 \ \)線式低圧電路があり,変圧器の中性点に\( \ \mathrm {B} \ \)種接地工事が施されている。\( \ \mathrm {B} \ \)種接地工事の接地抵抗値を\( \ R_{B} \ \mathrm {[\Omega ]} \ \),電路の一相当たりの対地静電容量を\( \ C \ \mathrm {[F]} \ \)とする。
この電路の絶縁抵抗が劣化により,電路の一相のみが絶縁抵抗値\( \ R_{G} \ \mathrm {[\Omega ]} \ \)に低下した。このとき,次の(a)及び(b)に答えよ。
ただし,上記以外のインピーダンスは無視するものとする。
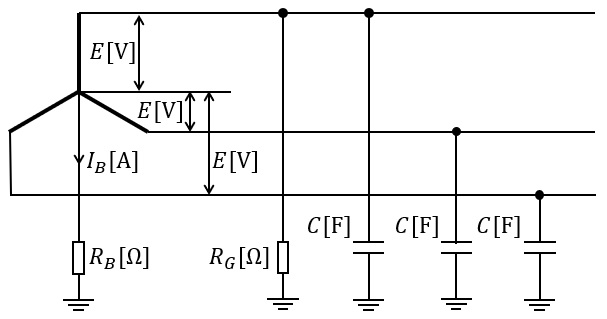
(a) 劣化により一相のみが絶縁抵抗値\( \ R_{G} \ \mathrm {[\Omega ]} \ \)に低下したとき,\( \ \mathrm {B} \ \)種接地工事の接地線に流れる電流の大きさを\( \ I_{B} \ \mathrm {[A]} \ \)とする。この\( \ I_{B} \ \)を表す式として,正しいのは次のうちどれか。
ただし,他の相の対地コンダクタンスは無視するものとする。
(1) \( \ \displaystyle \frac {E}{\sqrt {{R_{B}}^{2}+36\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \ \)
(2) \( \ \displaystyle \frac {3E}{\sqrt {\left( R_{G}+R_{B}\right) ^{2}+4\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \ \)
(3) \( \ \displaystyle \frac {E}{\sqrt {\left( R_{G}+R_{B}\right) ^{2}+4\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \ \)
(4) \( \ \displaystyle \frac {E}{\sqrt {{R_{G}}^{2}+36\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \ \)
(5) \( \ \displaystyle \frac {E}{\sqrt {\left( R_{G}+R_{B}\right) ^{2}+36\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \ \)
(b) 相電圧\( \ E \ \)を\( \ 100 \ \mathrm {[V]} \ \),周波数\( \ f \ \)を\( \ 50 \ \mathrm {[Hz]} \ \),対地静電容量\( \ C \ \)を\( \ 0.1 \ \mathrm {[\mu F]} \ \),絶縁抵抗値\( \ R_{G} \ \)を\( \ 100 \ \mathrm {[\Omega ]} \ \),接地抵抗値\( \ R_{B} \ \)を\( \ 15 \ \mathrm {[\Omega ]} \ \)とするとき,上記(a)の\( \ I_{B} \ \)の値として,最も近いのは次のうちどれか。
(1) \( \ 0.87 \ \) (2) \( \ 0.99 \ \) (3) \( \ 1.74 \ \) (4) \( \ 2.61 \ \) (5) \( \ 6.67 \ \)
【ワンポイント解説】
一線地絡事故発生時の\( \ \mathrm {B} \ \)種接地工事の接地線に流れる電流を求める問題です。(b)が比較的易しいので,非常に点数差が拡がりやすい問題です。
厳密にはテブナンの定理を検討して等価回路を考える問題ですが,時間的制約を考えて等価回路は覚えてしまっても良いかもしれません。
1.テブナンの定理
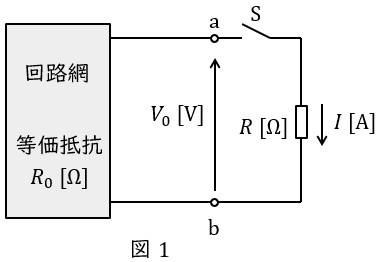
図1のような回路において,端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \),端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする(ただし,電圧源は短絡,電流源は開放する)と,図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。この関係は抵抗のみでなく,リアクタンスにも適用可能です。
2.配電線\( \ 1 \ \)線地絡時の等価回路
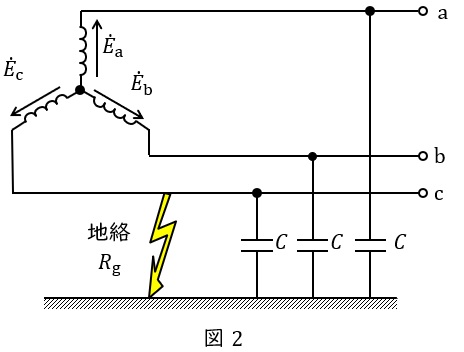
図2のような変圧器に接続された三相線路があり,\( \ \mathrm {c} \ \)相に\( \ 1 \ \)線地絡事故が発生したとします。
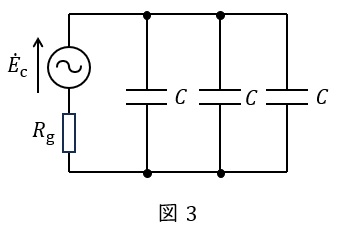
地絡点にテブナンの定理を適用すると,地絡点の開放電圧は\( \ {\dot E}_{\mathrm {c}} \ \),地絡点から見たインピーダンスは電源を短絡して考えれば良いので,各相の静電容量が並列に接続された状態となります。したがって,等価回路は図3のように描くことができます。
【解答】
(a)解答:(5)
地絡点の開放電圧\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {0}}&=&E \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
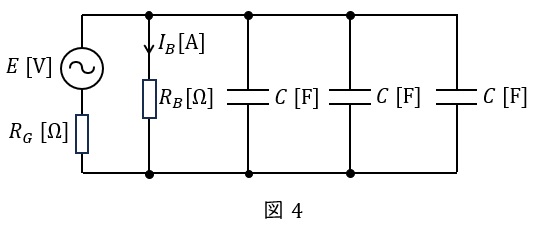
であり,ワンポイント解説「2.配電線\( \ 1 \ \)線地絡時の等価回路」に沿って地絡点から電源側を見たインピーダンスを検討すると\( \ R_{B} \ \)と各相の\( \ C \ \)が並列に接続されたインピーダンスとなるため,等価回路は図4のようになる。三相の並列の合成静電容量が\( \ 3C \ \mathrm {[F]} \ \)となることから,全体の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\dot Z&=&R_{G}+\frac {R_{B}\cdot \displaystyle \frac {1}{\mathrm {j}2\pi f \cdot 3C}}{R_{B}+\displaystyle \frac {1}{\mathrm {j}2\pi f \cdot 3C}} \\[ 5pt ]
&=&R_{G}+\frac {\displaystyle \frac {R_{B}}{\mathrm {j}6\pi fC}}{\displaystyle \frac {1+\mathrm {j}6\pi fCR_{B}}{\mathrm {j}6\pi fC}} \\[ 5pt ]
&=&R_{G}+\frac {R_{B}}{1+\mathrm {j}6\pi fCR_{B}} \\[ 5pt ]
&=&\frac {R_{B}+R_{G}+\mathrm {j}6\pi fCR_{B}R_{G}}{1+\mathrm {j}6\pi fCR_{B}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,地絡電流\( \ {\dot I}_{G} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{G}&=&\frac {E}{\dot Z} \\[ 5pt ]
&=&\frac {E}{\displaystyle \frac {R_{B}+R_{G}+\mathrm {j}6\pi fCR_{B}R_{G}}{1+\mathrm {j}6\pi fCR_{B}}} \\[ 5pt ]
&=&\frac {\left( 1+\mathrm {j}6\pi fCR_{B}\right) E}{R_{B}+R_{G}+\mathrm {j}6\pi fCR_{B}R_{G}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,分流の法則より,\( \ {\dot I}_{B} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{B}&=&\frac {\displaystyle \frac {1}{\mathrm {j}2\pi f \cdot 3C}}{R_{B}+\displaystyle \frac {1}{\mathrm {j}2\pi f \cdot 3C}}{\dot I}_{G} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{\mathrm {j}6\pi fC}}{R_{B}+\displaystyle \frac {1}{\mathrm {j}6\pi fC}}{\dot I}_{G} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{\mathrm {j}6\pi fC}}{\displaystyle \frac {1+\mathrm {j}6\pi fCR_{B}}{\mathrm {j}6\pi fC}}{\dot I}_{G} \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}6\pi fCR_{B}}{\dot I}_{G} \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}6\pi fCR_{B}}\times \frac {\left( 1+\mathrm {j}6\pi fCR_{B}\right) E}{R_{B}+R_{G}+\mathrm {j}6\pi fCR_{B}R_{G}} \\[ 5pt ]
&=& \frac {E}{R_{B}+R_{G}+\mathrm {j}6\pi fCR_{B}R_{G}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ I_{B} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{B}&=&\frac {E}{\sqrt {\left( R_{B}+R_{G}\right) ^{2}+36\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \\[ 5pt ]
&=&\frac {E}{\sqrt {\left( R_{G}+R_{B}\right) ^{2}+36\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
(a)解答式に各値を代入すると,
\[
\begin{eqnarray}
I_{B}&=&\frac {E}{\sqrt {\left( R_{G}+R_{B}\right) ^{2}+36\pi ^{2}f^{2}C^{2}{R_{B}}^{2}{R_{G}}^{2}}} \\[ 5pt ]
&=&\frac {100}{\sqrt {\left( 100+15\right) ^{2}+36\pi ^{2}\times 50^{2}\times \left( 0.1\times 10^{-6}\right)^{2}\times 15^{2}\times 100^{2}}} \\[ 5pt ]
&≒&\frac {100}{\sqrt {13 \ 225+0.02000}} \\[ 5pt ]
&≒&0.866 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは