Contents
【問題】
【難易度】★★★★☆(やや難しい)
分解能が\( \ 2 \ \mathrm {[mV]} \ \)の\( \ \mathrm {D-A} \ \)変換器について,図を参考にして次の(a)及び(b)に答えよ。
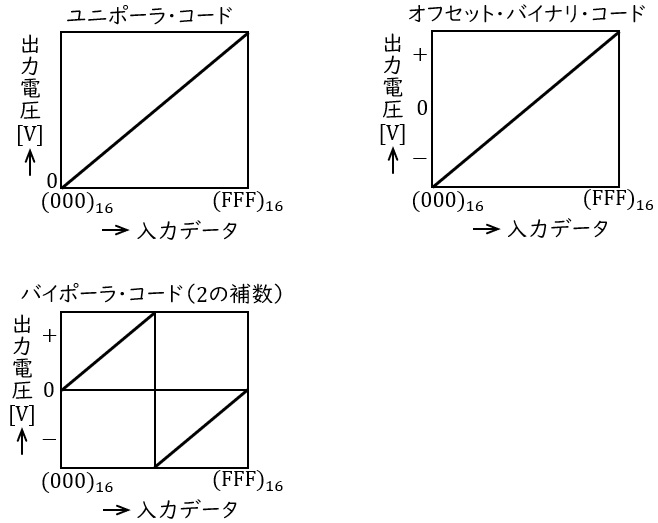
(a) \( \ 12 \ \)ビットのディジタル入力量の\( \ (000)_{16} \ \)を\( \ 0 \ \mathrm {[V]} \ \)の出力電圧として,正の電圧のみを扱うユニポーラ・コードによる\( \ \mathrm {D-A} \ \)変換器の場合,ディジタル入力量の\( \ \mathrm {(9C4)_{16}} \ \)は,\( \ \fbox { (ア) } \ \mathrm {[V]} \ \)の出力電圧になる。
ディジタル入力量の\( \ (000)_{16} \ \)から\( \ \mathrm {(FFF)_{16}} \ \)の範囲で,\( \ (800)_{16} \ \)を\( \ 0 \ \mathrm {[V]} \ \)の出力電圧とし,\( \ (000)_{16} \ \)側を負,\( \ \mathrm {(FFF)_{16}} \ \)側を正とするオフセット・バイナリ・コードによる\( \ \mathrm {D-A} \ \)変換器の場合,出力電圧の範囲は,\( \ \fbox { (イ) } \ \mathrm {[V]} \ \)となる。
また,\( \ 2 \ \)の補数を用いて正負の電圧を扱うバイポーラ・コードによる\( \ \mathrm {D-A} \ \)変換器では,ディジタル入力量の\( \ \mathrm {(A24)_{16}} \ \)は,\( \ \fbox { (ウ) } \ \mathrm {[V]} \ \)の出力電圧になる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる数値として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & 4.968 & -4.094 \sim 4.096 & -3.000 \\
\hline
(2) & 4.968 & -4.094 \sim 4.096 & -2.998 \\
\hline
(3) & 5.000 & -4.096 \sim 4.096 & -3.000 \\
\hline
(4) & 5.000 & -4.096 \sim 4.094 & -2.998 \\
\hline
(5) & 5.000 & -4.096 \sim 4.094 & -3.000 \\
\hline
\end{array}
\]
(b) この\( \ \mathrm {D-A} \ \)変換器がユニポーラ・コードの\( \ \mathrm {D-A} \ \)変換器の場合,出力電圧\( \ 1.250 \ \mathrm {[V]} \ \)を得るためのディジタル入力量は,\( \ \fbox { (エ) } \ \)となる。
この\( \ \mathrm {D-A} \ \)変換器がオフセット・バイナリ・コードの\( \ \mathrm {D-A} \ \)変換器の場合,出力電圧\( \ 1.250 \ \mathrm {[V]} \ \)を得るためのディジタル入力量は,\( \ \fbox { (オ) } \ \),出力電圧\( \ -1.250 \ \mathrm {[V]} \ \)を得るためのディジタル入力量は,\( \ \fbox { (カ) } \ \)となる。
この\( \ \mathrm {D-A} \ \)変換器が\( \ 2 \ \)の補数によるバイポーラ・コードの\( \ \mathrm {D-A} \ \)変換器の場合,出力電圧\( \ -1.250 \ \mathrm {[V]} \ \)を得るためのディジタル入力量は,\( \ \fbox { (キ) } \ \)となる。
上記の記述中の空白箇所(エ),(オ),(カ)及び(キ)に当てはまる数値として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (エ) & (オ) & (カ) & (キ) \\
\hline
(1) & \mathrm {(271)_{16}} & \mathrm {(A71)_{16}} & \mathrm {(58F)_{16}} & \mathrm {(D8F)_{16}} \\
\hline
(2) & \mathrm {(271)_{16}} & \mathrm {(271)_{16}} & \mathrm {(58F)_{16}} & \mathrm {(58F)_{16}} \\
\hline
(3) & \mathrm {(271)_{16}} & \mathrm {(A71)_{16}} & \mathrm {(D8F)_{16}} & \mathrm {(58F)_{16}} \\
\hline
(4) & \mathrm {(625)_{16}} & \mathrm {(271)_{16}} & \mathrm {(D8F)_{16}} & \mathrm {(D8F)_{16}} \\
\hline
(5) & \mathrm {(625)_{16}} & \mathrm {(A71)_{16}} & \mathrm {(D8F)_{16}} & \mathrm {(D8F)_{16}} \\
\hline
\end{array}
\]
【ワンポイント解説】
変換器で行われる出力電圧のアナログとディジタル換算を行う問題です。
(ウ)と(キ)の空欄の計算が難易度が高く,参考としている図が逆に引っかけとなっているので,受験生には厳しい問題であったかと思います。
1.主な進数の対応表
コンピュータ等のディジタル信号は主に\( \ 2 \ \)進数が使用されるため,電験でも基数変換は出題されます。
\( \ 2 \ \)進数,\( \ 8 \ \)進数,\( \ 10 \ \)進数,\( \ 16 \ \)進数の対応表は下表の通りとなります。表を覚えるのではなくルールを理解するようにしましょう。
\[
\begin{array}{|r|r|r|r|}
\hline
2 \ 進数 & 8 \ 進数 & 10 \ 進数 & 16 \ 進数 \\
\hline
0 & 0 & 0 & 0 \\
\hline
1 & 1 & 1 & 1 \\
\hline
10 & 2 & 2 & 2 \\
\hline
11 & 3 & 3 & 3 \\
\hline
100 & 4 & 4 & 4 \\
\hline
101 & 5 & 5 & 5 \\
\hline
110 & 6 & 6 & 6 \\
\hline
111 & 7 & 7 & 7 \\
\hline
1000 & 10 & 8 & 8 \\
\hline
1001 & 11 & 9 & 9 \\
\hline
1010 & 12 & 10 & \mathrm {A} \\
\hline
1011 & 13 & 11 & \mathrm {B} \\
\hline
1100 & 14 & 12 & \mathrm {C} \\
\hline
1101 & 15 & 13 & \mathrm {D} \\
\hline
1110 & 16 & 14 & \mathrm {E} \\
\hline
1111 & 17 & 15 & \mathrm {F} \\
\hline
10000 & 20 & 16 & 10 \\
\hline
\end{array}
\]
2.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換
\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換は,\( \ 2 \ \)で割った余りを下から順に並べると求められます。
具体的に\( \ 10 \ \)進数の\( \ \left( 30\right) _{10} \ \)を\( \ 2 \ \)進数へ変換すると,
\[
\begin{array}{cccc}
2) & 30 & & & \\
\hline
2) & 15 & \cdots & 0 \\
\hline
2) & 7 & \cdots & 1 \\
\hline
2) & 3 & \cdots & 1 \\
\hline
2) & 1 & \cdots & 1 \\
\hline
& 0 & \cdots & 1 \\
\end{array}
\]
ゆえに,
\[
\begin{eqnarray}
\left( 30\right) _{10} &=&\left( 11110\right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ 8 \ \)進数や\( \ 16 \ \)進数等任意の\( \ N \ \)進数への変換も同様に行うことができます。
3.\( \ 2 \ \)進数から\( \ 10 \ \)進数への変換
\( \ 2 \ \)進数を\( \ 10 \ \)進数にするためには各桁に\( \ 2^{x}(x=0,1,2・・・) \ \)乗をかけて導出できます。
例えば,\( \ 2 \ \)進数の\( \ \left( 101010\right) _{2} \ \)を\( \ 10 \ \)進数へ変換すると,
\[
\begin{eqnarray}
\left( 101010\right) _{2}&=&1\times 2^{5}+0\times 2^{4}+1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+0\times 2^{0} \\[ 5pt ]
&=&32+0+8+0+2+0 \\[ 5pt ]
&=&42 \\[ 5pt ]
\end{eqnarray}
\]
と求められます。\( \ 8 \ \)進数や\( \ 16 \ \)進数等任意の\( \ N \ \)進数も同様に求められます。
4.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換
\( \ 2 \ \)進数を\( \ 16 \ \)進数にするためには,\( \ 4 \ \)桁ごとに\( \ 16 \ \)進数に変換していきます。
例えば,\( \ 2 \ \)進数の\( \ \left( 11011010\right) _{2} \ \)を\( \ 16 \ \)進数へ変換すると,
\[
\begin{eqnarray}
\left( 1101\right) _{2}&=&\left( \mathrm {D}\right) _{16} \\[ 5pt ]
\left( 1010\right) _{2}&=&\left( \mathrm {A}\right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\left( 11011010\right) _{2}&=&\left( \mathrm {DA}\right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。\( \ 16 \ \)進数から\( \ 2 \ \)進数への変換も逆の操作により求めることができます。
5.補数
任意の\( \ N \ \)進数において,ある数に加えるとちょうど桁が上がる数を\( \ N \ \)の補数といい,例えば\( \ 10 \ \)進数でいうと,\( \ 3 \ \)と\( \ 7 \ \)や\( \ 4 \ \)と\( \ 6 \ \)となる関係を\( \ 10 \ \)の補数といいます。
\( \ 2 \ \)進数においては,例えば\( \ \left( 1001 \right) _{2} \ \)に\( \ \left( 0111 \right) _{2} \ \)を加えると\( \ \left( 10000 \right) _{2} \ \)になるため,\( \ \left( 0111 \right) _{2} \ \)は\( \ \left( 1001 \right) _{2} \ \)の\( \ 2 \ \)の補数といいます。
\( \ 2 \ \)の補数の求め方は,各桁を反転して\( \ 1 \ \)を加える下記手法が一般的です。
\[
\begin{array}{cccccc}
(元の数)& 1 & 0 & 0 & 1 & &\\[ 5pt ]
& 0 & 1 & 1 & 0 & ← &各桁反転 \\[ 5pt ]
( \ 2 \ の補数)& 0 & 1 & 1 & 1 & ← & \ 1 \ を加える \\[ 5pt ]
\end{array}
\]
【解答】
(a)解答:(5)
(ア)
\( \ \mathrm {(9C4)_{16}} \ \)を\( \ 10 \ \)進数に変換すると,ワンポイント解説「3.\( \ 2 \ \)進数から\( \ 10 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
\mathrm {\left( 9C4\right) }_{16}&=&9\times 16^{2}+12\times 16^{1}+4\times 16^{0} \\[ 5pt ]
&=&2 \ 304+192+4 \\[ 5pt ]
&=&2 \ 500 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 1 \ \)ビットあたり\( \ 2 \ \mathrm {[mV]} \ \)であるから,\( \ \mathrm {(9C4)_{16}} \ \)の出力電圧は,
\[
\begin{eqnarray}
2 \ 500 \times 2 \times 10^{-3}&=&5.000 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
\( \ \mathrm {(800)_{16}} \ \)と\( \ \mathrm {(FFF)_{16}} \ \)を\( \ 10 \ \)進数に変換すると,ワンポイント解説「3.\( \ 2 \ \)進数から\( \ 10 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
\mathrm {\left( 800\right) }_{16}&=&8\times 16^{2}+0\times 16^{1}+0\times 16^{0} \\[ 5pt ]
&=&2 \ 048+0+0 \\[ 5pt ]
&=&2 \ 048 \\[ 5pt ]
\mathrm { \left( FFF\right) }_{16}&=&15\times 16^{2}+15\times 16^{1}+15\times 16^{0} \\[ 5pt ]
&=&3 \ 840+240+15 \\[ 5pt ]
&=&4 \ 095 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 1 \ \)ビットあたり\( \ 2 \ \mathrm {[mV]} \ \)であるから,\( \ \mathrm {(000)_{16}} \ \)と\( \ \mathrm {(FFF)_{16}} \ \)の出力電圧は,
\[
\begin{eqnarray}
\left( 0-2 \ 048\right) \times 2 \times 10^{-3}&=&-4.096 \ \mathrm {[V]} \\[ 5pt ]
\left( 4 \ 095-2 \ 048\right) \times 2 \times 10^{-3}&=&4.094 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,出力電圧の範囲は,\( \ -4.096 \sim 4.094 \ \mathrm {[V]} \ \)と求められる。
(ウ)
\( \ \mathrm {(A24)_{16}} \ \)を\( \ 2 \ \)進数に変換すると,ワンポイント解説「4.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
\mathrm {\left( A24\right) }_{16}&=&\mathrm {\left( 1010 \ 0010 \ 0100 \right) }_{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ 2 \ \)の補数は,ワンポイント解説「5.補数」の通り,
\[
\begin{eqnarray}
\mathrm {\left( 0101 \ 1101 \ 1011 \right) }_{2} +\mathrm {\left( 0000 \ 0000 \ 0001 \right) }_{2} &=&\mathrm {\left( 0101 \ 1101 \ 1100 \right) }_{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。これを\( \ 10 \ \)進数に変換すると,ワンポイント解説「3.\( \ 2 \ \)進数から\( \ 10 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
\mathrm {\left( 0101 \ 1101 \ 1100 \right) }_{2} &=&1\times 2^{10}+1\times 2^{8}+1\times 2^{7}+1\times 2^{6}+1\times 2^{4}+1\times 2^{3}+1\times 2^{2} \\[ 5pt ]
&=&1 \ 024+256+128+64+16+8+4 \\[ 5pt ]
&=&1 \ 500 \\[ 5pt ]
\end{eqnarray}
\]
となるので,出力電圧は,
\[
\begin{eqnarray}
1 \ 500 \times \left( -2\times 10^{-3}\right) &=&-3.000 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
(エ)
\( \ 1 \ \)ビットあたり\( \ 2 \ \mathrm {[mV]} \ \)であるから,出力電圧\( \ 1.250 \ \mathrm {[V]} \ \)を\( \ 10 \ \)進数で表すと,
\[
\begin{eqnarray}
\frac {1.250}{2\times 10^{-3}} &=&625 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを\( \ 16 \ \)進数で表すと,ワンポイント解説「2.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換」の通り,
\[
\begin{array}{cccc}
16) & 625 & & & \\
\hline
16) & 39 & \cdots & 1 \\
\hline
16) & 2 & \cdots & 7 \\
\hline
& 0 & \cdots & 2 \\
\end{array}
\]
となるので,\( \ \mathrm {(271)_{16}} \ \)と求められる。
(オ)
(イ)の空欄で計算した通り\( \ \mathrm {(800)_{16}}=\mathrm {(2 \ 048)_{10}} \ \)であるから,出力電圧\( \ 1.250 \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
2 \ 048+625 &=&2 \ 673 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを\( \ 16 \ \)進数で表すと,ワンポイント解説「2.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換」の通り,
\[
\begin{array}{cccc}
16) & 2 \ 673 & & & \\
\hline
16) & 167 & \cdots & 1 \\
\hline
16) & 10 & \cdots & 7 \\
\hline
& 0 & \cdots & 10 \\
\end{array}
\]
となるので,\( \ \mathrm {(A71)_{16}} \ \)と求められる。
(カ)
(オ)と同様に,出力電圧\( \ -1.250 \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
2 \ 048-625 &=&1 \ 423 \\[ 5pt ]
\end{eqnarray}
\]
となり,これを\( \ 16 \ \)進数で表すと,ワンポイント解説「2.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換」の通り,
\[
\begin{array}{cccc}
16) & 1 \ 423 & & & \\
\hline
16) & 88 & \cdots & 15 \\
\hline
16) & 5 & \cdots & 8 \\
\hline
& 0 & \cdots & 5 \\
\end{array}
\]
となるので,\( \ \mathrm {(58F)_{16}} \ \)と求められる。
(キ)
出力電圧\( \ -1.250 \ \mathrm {[V]} \ \)を\( \ 10 \ \)進数で表すと,
\[
\begin{eqnarray}
\frac {-1.250}{-2\times 10^{-3}} &=&625 \\[ 5pt ]
\end{eqnarray}
\]
であり,これを\( \ 2 \ \)進数で表すと,ワンポイント解説「2.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換」の通り,
\[
\begin{array}{cccc}
2) & 625 & & & \\
\hline
2) & 312 & \cdots & 1 \\
\hline
2) & 156 & \cdots & 0 \\
\hline
2) & 78 & \cdots & 0 \\
\hline
2) & 39 & \cdots & 0 \\
\hline
2) & 19 & \cdots & 1 \\
\hline
2) & 9 & \cdots & 1 \\
\hline
2) & 4 & \cdots & 1 \\
\hline
2) & 2 & \cdots & 0 \\
\hline
2) & 1 & \cdots & 0 \\
\hline
& 0 & \cdots & 1 \\
\end{array}
\]
となるので,\( \ \mathrm {(0010 \ 0111 \ 0001)_{2}} \ \)となる。これの\( \ 2 \ \)の補数は,ワンポイント解説「5.補数」の通り,
\[
\begin{eqnarray}
\mathrm {\left( 1101 \ 1000 \ 1110 \right) }_{2} +\mathrm {\left( 0000 \ 0000 \ 0001 \right) }_{2} &=&\mathrm {\left( 1101 \ 1000 \ 1111 \right) }_{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを\( \ 16 \ \)進数で表すと,ワンポイント解説「4.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換」の通り,
\[
\begin{eqnarray}
\mathrm {\left( 1101 \ 1000 \ 1111 \right) }_{2} &=&\mathrm {\left( D8F \right) }_{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは