《機械》〈直流機〉[H20:問2]負荷が変化したときの直流分巻電動機の逆起電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格出力\( \ 5 \ \mathrm {[kW]} \ \)，定格電圧\( \ 220 \ \mathrm {[V]} \ \)の直流分巻電動機がある。この電動機を定格電圧で運転したとき，電機子電流が\( \ 23.6 \ \mathrm {[A]} \ \)で定格出力を得た。この電動機をある負荷に対して定格電圧で運転したとき，電機子電流が\( \ 20 \ \mathrm {[A]} \ \)になった。このときの逆起電力（誘導起電力）\( \ \mathrm {[V]} \ \)の値として，最も近いのは次のうちどれか。

ただし，電機子反作用はなく，ブラシの抵抗は無視できるものとする。

　(1)　\( \ 201 \ \)　　(2)　\( \ 206 \ \)　　(3)　\( \ 213 \ \)　　(4)　\( \ 218 \ \)　　(5)　\( \ 227 \ \)

【ワンポイント解説】

直流分巻電動機の負荷が変動した際の逆起電力の変化を問う問題です。
ほぼ毎年のように直流電動機の問題は出題されますので，等価回路と関係式は扱えるようにしておきましょう。

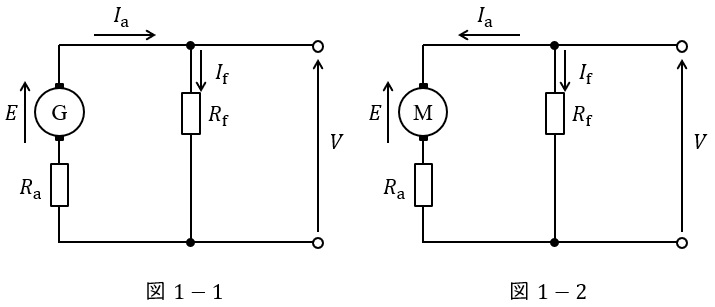
1.直流分巻発電機及び電動機の等価回路と特性
分巻発電機の等価回路を図1-1，分巻電動機の等価回路を図1-2に示します。ただし，図において，\( \ E \ \mathrm {[V]} \ \)は誘導起電力(電動機の場合は逆起電力)，\( \ V \ \mathrm {[V]} \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \mathrm {[\Omega ]} \ \)は界磁抵抗です。
界磁を同じ電源から得る自励式ですが，界磁回路が電機子回路に並列に接続されているのが特徴です。
等価回路より，分巻発電機においては，
\[
\begin{eqnarray}
E &=&V+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] 分巻電動機においては，
\[
\begin{eqnarray}
V &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。

磁束を\( \ \phi \ \mathrm {[Wb]} \ \)，回転速度を\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，\( \ \phi ∝ I_{\mathrm {f}} \ \)となるので，誘導起電力(逆起電力)\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {f}} N \\[ 5pt ] \end{eqnarray}
\] となります。またトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.直流分巻電動機の出力
電動機の角速度が\( \ \displaystyle \omega =\frac {2\pi N}{60} \ \mathrm {[rad / s]} \ \)，トルクが\( \ T \ \mathrm {[N\cdot m]} \ \)， 誘導起電力(逆起電力)が\( \ E \ \mathrm {[V]} \ \)，電機子電流\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)が与えられているとき，出力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&\omega T \\[ 5pt ] &=&EI_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(3)
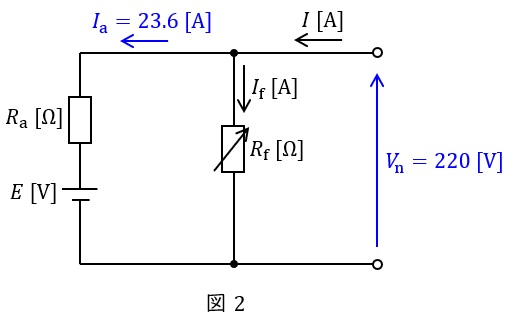
題意に沿って等価回路を描くと図2のようになる。
定格出力\( \ P_{\mathrm {n}}=5 \ \mathrm {[kW]} \ \)で運転したときの電機子電流が\( \ I_{\mathrm {a}}=23.6 \ \mathrm {[A]} \ \)なので，逆起電力\( \ E \ \mathrm {[V]} \ \)は，ワンポイント解説「2.直流分巻電動機の出力」の通り，
\[
\begin{eqnarray}
E &=&\frac {P_{\mathrm {n}}}{I_{\mathrm {a}}} \\[ 5pt ] &=&\frac {5\times 10^{3}}{23.6} \\[ 5pt ] &≒&211.9 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，定格電圧\( \ V_{\mathrm {n}}=220 \ \mathrm {[V]} \ \)と誘導起電力の関係より，電機子抵抗\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)の大きさは，ワンポイント解説「1.直流分巻発電機及び電動機の等価回路と特性」の通り，
\[
\begin{eqnarray}
V_{\mathrm {n}} &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] R_{\mathrm {a}}I_{\mathrm {a}} &=&V_{\mathrm {n}}-E \\[ 5pt ] R_{\mathrm {a}} &=&\frac {V_{\mathrm {n}}-E}{I_{\mathrm {a}}} \\[ 5pt ] &=&\frac {220-211.9}{23.6} \\[ 5pt ] &≒&0.3432 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，電機子電流が\( \ I_{\mathrm {a}}^{\prime }=20 \ \mathrm {[A]} \ \)となったときの逆起電力\( \ E^{\prime } \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E^{\prime } &=&V_{\mathrm {n}} -R_{\mathrm {a}}I_{\mathrm {a}}^{\prime } \\[ 5pt ] &=&220 -0.3432\times 20 \\[ 5pt ] &≒&213 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。