《機械》〈回転機〉[H27:問15]誘導電動機の諸計算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

定格出力\( \ 15 \ \mathrm {kW} \ \)，定格電圧\( \ 220 \ \mathrm {V} \ \)，定格周波数\( \ 60 \ \mathrm {Hz} \ \)，\( \ 6 \ \)極の三相巻線形誘導電動機がある。二次巻線は星形(\( \ \mathrm {Y} \ \))結線でスリップリングを通して短絡されており，各相の抵抗値は\( \ 0.5 \ \Omega \ \)である。この電動機を定格電圧，定格周波数の電源に接続して定格出力(このときの負荷トルクを\( \ T_{\mathrm {n}} \ \)とする)で運転しているときの滑りは\( \ 5 \ ％ \ \)であった。

計算に当たっては，\( \ \mathrm {L} \ \)形簡易等価回路を採用し，機械損及び鉄損は無視できるものとして，次の(a)及び(b)の問に答えよ。

(a)　速度を変えるために，この電動機の二次回路の各相に\( \ 0.2 \ \Omega \ \)の抵抗を直列に挿入し，上記と同様に定格電圧，定格周波数の電源に接続して上記と同じ負荷トルク\( \ T_{\mathrm {n}} \ \)で運転した。このときの滑りの値\( \ [％] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 3.0 \ \)　　(2)　\( \ 3.6 \ \)　　(3)　\( \ 5.0 \ \)　　(4)　\( \ 7.0 \ \)　　(5)　\( \ 10.0 \ \)

(b)　電動機の二次回路の各相に上記(a)と同様に\( \ 0.2 \ \Omega \ \)の抵抗を直列に挿入したままで，電源の周波数を変えずに電圧だけを\( \ 200 \ \mathrm {V} \ \)に変更したところ，ある負荷トルクで安定に運転した。このときの滑りは上記(a)と同じであった。
　この安定に運転したときの負荷トルクの値\( \ \mathrm{[N\cdot m]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 99 \ \)　　(2)　\( \ 104 \ \)　　(3)　\( \ 106 \ \)　　(4)　\( \ 109 \ \)　　(5)　\( \ 114 \ \) 　

【ワンポイント解説】

やや計算が複雑な問題ですが，誘導電動機の問題は計算のパターンが少なく，試験にも類題がよく出題されるので，試験日までには確実に理解しておきたいところです。

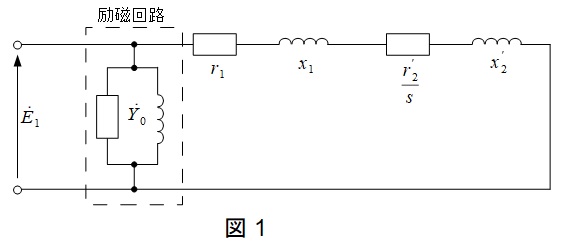
1.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は，図1のようになります。

2.巻線形誘導電動機の比例推移
巻線形誘導電動機においては，トルク一定の下で二次抵抗と滑りが比例するという性質を持ち，これを比例推移と言います。

【解答】

(a)解答：(4)
ワンポイント解説「2.巻線形誘導電動機の比例推移」より，負荷トルク\( \ T_{\mathrm {n}} \ \)のまま，二次抵抗を\( \ 0.5 \ \Omega \ \)から\( \ 0.7 \ \Omega \ \)に変化させたので，このときの滑りの値\( \ s \ \)は，
\[
\begin{eqnarray}
\frac {s}{5}&=&\frac {0.7}{0.5}\\[ 5pt ] s&=&7 \ [％] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
この電動機の同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}}&=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 60}{6} \\[ 5pt ] &=&1200 \ \mathrm {[min ^{-1}]} \\[ 5pt ] \end{eqnarray}
\] であるから，この電動機の初期状態の回転速度\( \ N \ \)は，
\[
\begin{eqnarray}
N&=&N_{\mathrm {s}}(1-s) \\[ 5pt ] &=&1200 \times (1-0.05) \\[ 5pt ] &=&1140 \ \mathrm {[min ^{-1}]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，この時の負荷トルク\( \ T_{\mathrm {n}} \ \)は，\( \ P_{\mathrm {n}}=15 \ \mathrm {kW} \ \)，\( \ \displaystyle \omega =\frac {2\pi N}{60} \ \)であるから，
\[
\begin{eqnarray}
T_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\omega } \\[ 5pt ] &=&\frac {P_{\mathrm {n}}}{\displaystyle \frac {2\pi N}{60}} \\[ 5pt ] &=&\frac {15\times 10^{3}}{\displaystyle \frac {2\pi \times 1140}{60}} \\[ 5pt ] &≒&125.6 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] となる。
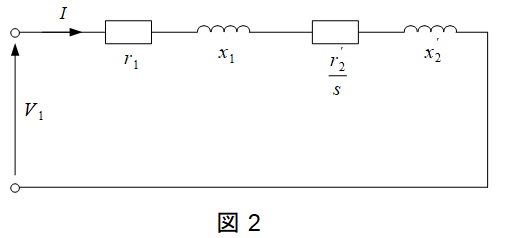
また，題意より機械損，鉄損は無視できるので，\( \ \mathrm {L} \ \)形等価回路を描くと図2のようになる。
図2より，電動機の二次電流\( \ I \ \)の大きさは，
\[
I=\frac {V_{1}}{\displaystyle \sqrt {\left( r_{1}+\frac {{r_{2}}^{\prime }}{s}\right) ^{2} +\left( x_{1}+{x_{2}}^{\prime } \right) ^{2}}}
\] となるので，二次入力の大きさ\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}}{s}I^{2} \\[ 5pt ] &=&\frac {3r_{2}V_{1}^{2}}{\displaystyle s\left[ \left( r_{1}+\frac {{r_{2}}^{\prime }}{s}\right) ^{2} +\left( x_{1}+{x_{2}}^{\prime } \right) ^{2}\right] } \\[ 5pt ] \end{eqnarray}
\] となるので，トルクの大きさ\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {P_{2}}{\omega } \\[ 5pt ] &=&\frac {3r_{2}V_{1}^{2}}{\displaystyle \omega s\left[ \left( r_{1}+\frac {{r_{2}}^{\prime }}{s}\right) ^{2} +\left( x_{1}+{x_{2}}^{\prime } \right) ^{2}\right] } \\[ 5pt ] \end{eqnarray}
\] となり，\( \ T∝V^{2} \ \)の関係であることが分かる。
よって，電圧を\( \ 220 \ \mathrm {V} \ \)から\( \ 200 \ \mathrm {V} \ \)に変更したので，安定した時の負荷トルクの値\( \ T \ \)は，
\[
\begin{eqnarray}
\frac {T}{T_{\mathrm {n}}}&=&\left( \frac {200}{220 }\right) ^{2} \\[ 5pt ] T&=&\left( \frac {200}{220 }\right) ^{2}T_{\mathrm {n}} \\[ 5pt ] &=&\left( \frac {200}{220 }\right) ^{2}\times 125.6 \\[ 5pt ] &≒&104 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。