《機械》〈情報伝送及び処理〉[H28:問14]基数変換に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，基数の変換に関する記述である。

・\( \ 2 \ \)進数\( \ \mathrm {00100100} \ \)を\( \ 10 \ \)進数で表現すると\( \ \fbox {　 （ア） 　} \ \)である。
・\( \ 10 \ \)進数\( \ \mathrm {170} \ \)を\( \ 2 \ \)進数で表現すると\( \ \fbox {　 （イ） 　} \ \)である。
・\( \ 2 \ \)進数\( \ \mathrm {111011100001} \ \)を\( \ 8 \ \)進数で表現すると\( \ \fbox {　 （ウ） 　} \ \)である。
・\( \ 16 \ \)進数\( \ \fbox {　 （エ） 　} \ \)を\( \ 2 \ \)進数で表現すると\( \ \mathrm {11010111} \ \)である。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 36 & 10101010 & 7321 & \mathrm {D7} \\
\hline
(2) & 37 & 11010100 & 7341 & \mathrm {C7} \\
\hline
(3) & 36 & 11010100 & 7341 & \mathrm {D7} \\
\hline
(4) & 36 & 10101010 & 7341 & \mathrm {D7} \\
\hline
(5) & 37 & 11010100 & 7321 & \mathrm {C7} \\
\hline
\end{array}
\]

【ワンポイント解説】

基数変換は暗記するしかないため，難しく感じるかもしれませんが，マスターすると確実に点数が取れます。本問を通じて，あらゆる変換をマスターして下さい。参考に各進数の対応表を示します。

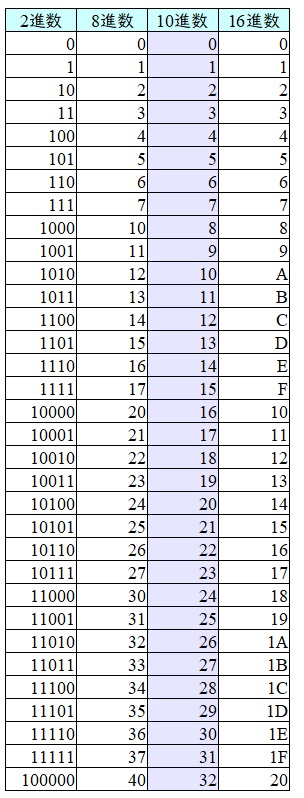
【解答】

解答：(4)
(ア)
\( \ 2 \ \)進数を\( \ 10 \ \)進数にするためには各桁に\( \ 2^{x}(x=0,1,2・・・) \ \)乗をかけて導出します。具体的には，
\[
\begin{eqnarray}
\left( 00100100\right) _{2} &=&0\times 2^{7} +0\times 2^{6}+1\times 2^{5}+0\times 2^{4}+0\times 2^{3}+1\times 2^{2}+0\times 2^{1}+0\times 2^{0} \\[ 5pt ] &=&0+0+32+0+0+4+0+0 \\[ 5pt ] &=&36
\end{eqnarray}
\] と求められます。

(イ)
\( \ 10 \ \)進数を\( \ 2 \ \)進数にするためには，\( \ 10 \ \)進数を\( \ 2 \ \)で割っていき，その余りの数を下から並べると求められます。

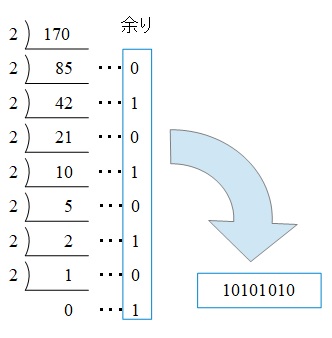
どうしても上記の方法を思い出せない場合は(ア)と同じように，解答の各\( \ 2 \ \)進数を\( \ 10 \ \)進数にすることで求めることもできます。
\[
\begin{eqnarray}
\left( 10101010\right) _{2} &=&1\times 2^{7} +0\times 2^{6}+1\times 2^{5}+0\times 2^{4}+1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+0\times 2^{0} \\[ 5pt ] &=&128+0+32+0+8+0+2+0 \\[ 5pt ] &=&170
\end{eqnarray}
\] \[
\begin{eqnarray}
\left( 11010100\right) _{2} &=&1\times 2^{7} +1\times 2^{6}+0\times 2^{5}+1\times 2^{4}+0\times 2^{3}+1\times 2^{2}+0\times 2^{1}+0\times 2^{0} \\[ 5pt ] &=&128+64+0+16+0+4+0+0 \\[ 5pt ] &=&212
\end{eqnarray}
\]

(ウ)
\( \ 2 \ \)進数を\( \ 8 \ \)進数にするためには，\( \ 2 \ \)進数を\( \ 3 \ \)桁ずつ分け，それぞれを数値で出すことで求められます。

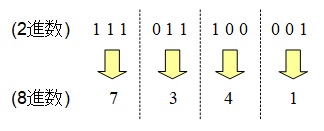
この解法も忘れてしまった時はどちらも10進数にすることで求めることもできます。
\[
\begin{eqnarray}
\left( 111011100001\right) _{2} &=&1\times 2^{11} +1\times 2^{10} +1\times 2^{9} +0\times 2^{8} +1\times 2^{7} +1\times 2^{6} \\[ 5pt ] &+&1\times 2^{5}+0\times 2^{4}+0\times 2^{3}+0\times 2^{2}+0\times 2^{1}+1\times 2^{0} \\[ 5pt ] &=&2048+1024+512+0+128+64+32+0+0+0+0+1 \\[ 5pt ] &=&3809
\end{eqnarray}
\] \[
\begin{eqnarray}
\left( 7321\right) _{8} &=&7\times 8^{3} +3\times 8^{2} +2\times 8^{1} +1\times 8^{0} \\[ 5pt ] &=&3584+192+16+1 \\[ 5pt ] &=&3793
\end{eqnarray}
\] \[
\begin{eqnarray}
\left( 7341\right) _{8} &=&7\times 8^{3} +3\times 8^{2} +4\times 8^{1} +1\times 8^{0} \\[ 5pt ] &=&3584+192+32+1 \\[ 5pt ] &=&3809
\end{eqnarray}
\]

(エ)
\( \ 2 \ \)進数を\( \ 16 \ \)進数にするためには，\( \ 2 \ \)進数を\( \ 4 \ \)桁ずつ分け，それぞれを数値で出すことで求められます。

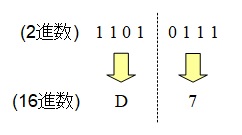
\( \ 2 \ \)進数や\( \ 8 \ \)進数と同じように\( \ 16 \ \)進数でも同じような計算ができます。ただし，英字がいくつであるかは知っている必要があります。
\[
\begin{eqnarray}
\left( 11010111\right) _{2} &=&1\times 2^{7} +1\times 2^{6}+0\times 2^{5}+1\times 2^{4}+0\times 2^{3}+1\times 2^{2}+1\times 2^{1}+1\times 2^{0} \\[ 5pt ] &=&128+64+0+16+0+4+2+1 \\[ 5pt ] &=&215
\end{eqnarray}
\] \[
\begin{eqnarray}
\left( \mathrm{C}7\right) _{16} &=&\mathrm{C}(12)\times 16^{1} +7\times 16^{0} \\[ 5pt ] &=&192+7 \\[ 5pt ] &=&199
\end{eqnarray}
\] \[
\begin{eqnarray}
\left( \mathrm{D}7\right) _{16} &=&\mathrm{D}(13)\times 16^{1} +7\times 16^{0} \\[ 5pt ] &=&212+3 \\[ 5pt ] &=&215
\end{eqnarray}
\]