Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,誘導機に関する記述である。
誘導機の二次入力は\( \ \fbox { (ア) } \ \)とも呼ばれ,トルクに比例する。二次入力における機械出力と二次銅損の比は,誘導機の滑りを\( \ s \ \)として\( \ \fbox { (イ) } \ \)の関係にある。この関係を用いると,二次銅損は常に正であることから,\( \ s \ \)が\( \ -1 \ \)から\( \ 0 \ \)の間の値をとるとき機械出力は\( \ \fbox { (ウ) } \ \)となり,誘導機は\( \ \fbox { (エ) } \ \)として運転される。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 同期ワット & (1-s):s & 負 & 発電機 \\
\hline
(2) & 同期ワット & (1+s):s & 負 & 発電機 \\
\hline
(3) & トルクワット & (1+s):s & 正 & 電動機 \\
\hline
(4) & 同期ワット & (1-s):s & 負 & 電動機 \\
\hline
(5) & トルクワット & (1-s):s & 正 & 電動機 \\
\hline
\end{array}
\]
【ワンポイント解説】
三相誘導電動機の等価回路は描けるようにしておく必要があります。誘導機は計算問題も穴埋め問題も多数出題されるため,ぜひマスターして得点源としたいところです。
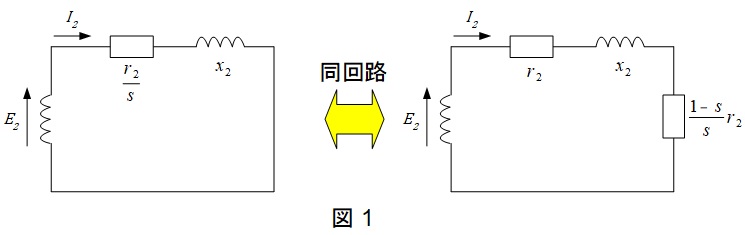
1.三相誘導電動機の\( \ 1 \ \)相分の二次側等価回路
図1が三相誘導電動機の\( \ 1 \ \)相分の二次側等価回路となります。滑り\( \ s \ \)で運転する時,二次誘導起電力\( \ E_{2} \ \)と漏れリアクタンス\( \ x_{2} \ \)は\( \ s \ \)倍となります。回路全体を\( \ s \ \)で割り,等価回路を描くと図1左のようになり,銅損分\( \ r_{2} \ \)を取り出すと図1右のような回路となります。従って,二次入力\( \ P_{2} \ \),二次銅損\( \ P_{\mathrm {C2}} \ \),機械的出力\( \ P_{\mathrm {M}} \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {C2}}&=&r_{2}I_{2}^{2}\\[ 5pt ]
P_{\mathrm {M}}&=&\frac {1-s}{s} r_{2}I_{2}^{2}\\[ 5pt ]
P_{2}&=&P_{\mathrm {C2}}+P_{\mathrm {M}}=\frac {r_{2}}{s} I_{2}^{2}\\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {C2}}:P_{\mathrm {M}}=\frac {1}{s}:1:\frac {1-s}{s}=1:s:(1-s)\\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
(ア)
同期ワットは同期速度で運転した時の出力で,二次入力と等しくなります。
(イ)
ワンポイント解説「1.三相誘導電動機の\( \ 1 \ \)相分の二次側等価回路」の通り,機械的出力と二次銅損の比は\( \ (1-s):s \ \)となります。
(ウ)
ワンポイント解説「1.三相誘導電動機の\( \ 1 \ \)相分の二次側等価回路」の通り,\( \ P_{\mathrm {M}} \ \)の\( \ s \ \)に負の値を代入すると,\( \ P_{\mathrm {M}} \ \)も負となります。
(エ)
機械的出力が負となるので,発電機として運転されることになります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは