Contents
【問題】
【難易度】★★★☆☆(普通)
定格出力\( \ 11.0 \ \mathrm {kW} \ \),定格電圧\( \ 220 \ \mathrm {V} \ \)の三相かご形誘導電動機が定トルク負荷に接続されており,定格電圧かつ定格負荷において滑り\( \ 3.0 \ \mathrm {%} \ \)で運転されていたが,電源電圧が低下し滑りが\( \ 6.0 \ \mathrm {%} \ \)で一定となった。滑りが一定となったときの負荷トルクは定格電圧のときと同じであった。このとき,二次電流の値は定格電圧のときの何倍になるか。最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,電源周波数は定格値で一定とする。
(1) \(0.50\) (2) \(0.97\) (3) \(1.03\) (4) \(1.41\) (5) \(2.00\)
【ワンポイント解説】
誘導電動機に関する問題です。誘導電動機の問題が出題されたら,まず等価回路を描くことが重要となります。トルクの導出は非常によく出題される内容となります。ほぼ数値は同じものを使用しますので確実に導出できるようにして下さい。
1.誘導電動機の\(\mathrm {L}\)形等価回路
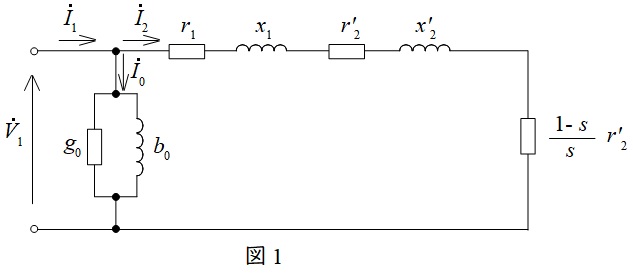
誘導電動機の等価回路は図1のようになります。ここで\({\dot V}_{1}\)は一次電圧,\({\dot I}_{1}\)は一次電流,\({\dot I}_{0}\)は励磁電流,\({\dot I}_{2}\)は二次電流,\(r_{1}\)は一次巻線抵抗,\(r_{2}^{\prime }\)は二次抵抗の一次換算値,\(x_{1}\)は一次漏れリアクタンス,\(x_{2}^{\prime }\)は二次漏れリアクタンスの一次換算値,\(s\)は滑りとなります。
【解答】
解答:(4)
図1の\(\mathrm {L}\)形等価回路において,滑り\(s\)で運転しているとすると,二次入力\(P_{2}\)は,
\[
\begin{eqnarray}
P_{2} &=&3\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,トルク\(T\)は,定格角周波数を\(\displaystyle \omega _{\mathrm {s}}=\frac {2\pi N _{\mathrm {s}}}{60}\)(\(N _{\mathrm {s}}\)は同期速度)とすると,
\[
\begin{eqnarray}
T &=&\frac {P}{\omega } \\[ 5pt ]
&=&\frac {P_{2}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime }I_{2}^{2}}{s\omega _{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,滑り\( \ s_{1}=3.0 \ \mathrm {%} \ \)の時の二次電流の値を\(I_{21}\),滑り\( \ s_{2}=6.0 \ \mathrm {%} \ \)の時の二次電流の値を\(I_{22}\)とすると,負荷トルクは変化していないので,
\[
\begin{eqnarray}
\frac {3r_{2}^{\prime }I_{21}^{2}}{s_{1}\omega _{\mathrm {s}}} &=&\frac {3r_{2}^{\prime }I_{22}^{2}}{s_{2}\omega _{\mathrm {s}}} \\[ 5pt ]
\frac {I_{21}^{2}}{s_{1}} &=&\frac {I_{22}^{2}}{s_{2}} \\[ 5pt ]
I_{22}&=&\sqrt {\frac {s_{2}}{s_{1}}}I_{21} \\[ 5pt ]
&=&\sqrt {\frac {0.06}{0.03}}I_{21} \\[ 5pt ]
&≒&1.41I_{21} \\[ 5pt ]
\end{eqnarray}
\]
となり,\(1.41\)倍と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは