Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
消費電力\( \ 1.00 \ \mathrm {kW} \ \)のヒートポンプ式電気給湯器を\( \ 6 \ \)時間運転して,温度\( \ 20.0 \ \mathrm {℃} \ \),体積\( \ 0.370 \ \mathrm {m^{3}} \ \)の水を加熱した。ここで用いられているヒートポンプユニットの成績係数(\( \ \mathrm {COP} \ \))は\( \ 4.5 \ \)である。次の(a)及び(b)の問に答えよ。
ただし,水の比熱容量と密度は,それぞれ,\( \ 4.18\times 10^{3} \ \mathrm {J / \left( kg\cdot K\right) } \ \)と\( \ 1.00\times 10^{3} \ \mathrm {kg / m^{3}} \ \)とし,水の温度に関係なく一定とする。ヒートポンプ式電気給湯器の貯湯タンク,ヒートポンプユニット,配管などの加熱に必要な熱エネルギーは無視し,それらからの熱損失もないものとする。また,ヒートポンプユニットの消費電力及び\( \ \mathrm {COP} \ \)は,いずれも加熱の開始から終了まで一定とする。
(a) このときの水の加熱に用いた熱エネルギーの値\( \ \mathrm {[MJ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 21.6 \ \) (2) \( \ 48.6 \ \) (3) \( \ 72.9 \ \) (4) \( \ 81.0 \ \) (5) \( \ 97.2 \ \)
(b) 加熱後の水の温度[℃]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 34.0 \ \) (2) \( \ 51.4 \ \) (3) \( \ 67.1 \ \) (4) \( \ 72.4 \ \) (5) \( \ 82.8 \ \)
【ワンポイント解説】
ヒートポンプを使用した電気給湯器の加温に関する問題です。
ヒートポンプでは冷媒の特性を利用して消費電力以上の熱エネルギーを水に与えることができます。
本問ではあまり知識として必要はないですが,ヒートポンプの仕組みや暖房時と冷房時の成績係数の違い等は重要な内容となりますので,理解しておくようにして下さい。
また,本問の令和元年問17に類題がありますので,確認しておくようにしましょう。
1.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換
単位の定義より,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ/s]} &=&1 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,両辺の単位に\( \ \mathrm {[s]} \ \)をかけると,
\[
\begin{eqnarray}
1 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot s]} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺に\( \ 1 \ \mathrm {[h]}=3600 \ \mathrm {[s]} \ \)を考慮して,\( \ 3600 \ \)をかけると,
\[
\begin{eqnarray}
3 \ 600 \ \mathrm {[kJ]} &=&1 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.ヒートポンプの構成機器
ヒートポンプのフローを図1に示します。冷房時が青線,暖房時は赤線の流れとなります。冷房時を例に示します。
蒸発器:膨張弁からの低温低圧の液を蒸発させ気化させます。
四方弁:暖房冷房時に圧縮機に流れる媒体の向きを同じにするために向きを変えるものです。
圧縮機:蒸発器から出た低圧の蒸気を高圧蒸気にします。
凝縮器:圧縮機で高温高圧となった蒸気を凝縮し,液化させます。
膨張弁:凝縮器から出た液を膨張し,低温低圧の液にします。
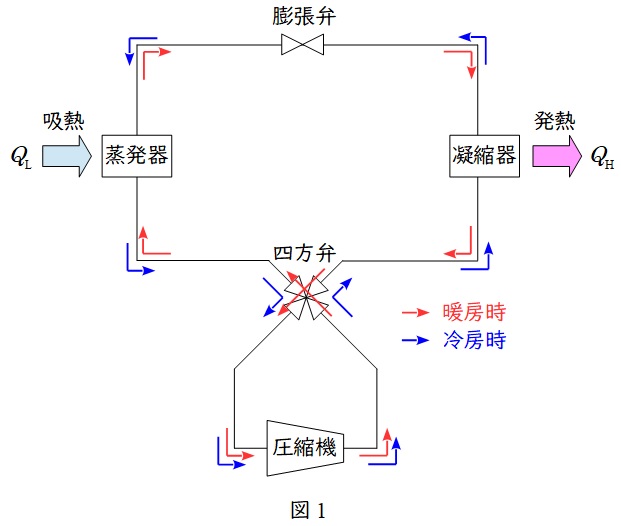
※図1において,暖房時には熱交換器である蒸発器と凝縮器の役割が逆となります。
3.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))
図1において,蒸発器の吸熱量\( \ Q_{\mathrm {L}} \ \)及び圧縮機にかける仕事量\( \ W \ \)と凝縮器の放熱量\( \ Q_{\mathrm {H}} \ \)は等しいので,
\[
\begin{eqnarray}
Q_{\mathrm {H}}&=&Q_{\mathrm {L}}+W \\[ 5pt ]
\end{eqnarray}
\]
という関係があり,冷房時と暖房時の成績係数\( \ \mathrm {{COP}_{L}} \ \),\( \ \mathrm {{COP}_{H}} \ \)は,
\[
\begin{eqnarray}
\mathrm {{COP}_{L}}&=&\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\mathrm {{COP}_{H}}&=&\frac {Q_{\mathrm {H}}}{W} \\[ 5pt ]
&=&\frac {Q_{\mathrm {L}}+W}{W} \\[ 5pt ]
&=&1+\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.水の温度上昇と必要なエネルギーの関係
水にエネルギー\( \ Q \ \mathrm {[J]} \ \)を加えたときの温度上昇値\( \ \Delta T \ \mathrm {[K]} \ \)には,質量\( \ m \ \mathrm {[kg]} \ \),比熱容量\( \ c \ \mathrm {[J / \left( kg\cdot K\right) ]} \ \)とすると
\[
\begin{eqnarray}
Q &=&mc \Delta T \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(a)解答:(5)
消費電力\( \ P=1.00 \ \mathrm {[kW]} \ \)のヒートポンプ式電気給湯器を\( \ t=6 \ \mathrm {[h]} \ \)運転したときの消費電力量の熱量換算\( \ W \ \mathrm {[kJ]} \ \)は,ワンポイント解説「1.\( \ \mathrm {[kJ]} \ \)と\( \ \mathrm {[kW\cdot h]} \ \)の変換」の通り,
\[
\begin{eqnarray}
W&=&Pt\times 3 \ 600 \\[ 5pt ]
&=&1.00\times 6\times 3 \ 600 \\[ 5pt ]
&=&21 \ 600 \ \mathrm {[kJ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,成績係数\( \ \mathrm {COP}=4.5 \ \)であることから,水の加熱に使われた熱エネルギー\( \ Q \ \mathrm {[MJ]} \ \)は,ワンポイント解説「3.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))」より,
\[
\begin{eqnarray}
Q&=&\mathrm {COP}\cdot W \\[ 5pt ]
&=&4.5\times 21 \ 600 \\[ 5pt ]
&=&97 \ 200 \ \mathrm {[kJ]} → 97.2 \ \mathrm {[MJ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(5)
加温後の水の温度\( \ T_{2} \ \mathrm {[℃]} \ \)は,加温前の温度\( \ T_{1}=20.0 \ \mathrm {[℃]} \ \),体積\( \ V=0.370 \ \mathrm {[m^{3}]} \ \),比熱容量\( \ c=4.18\times 10^{3} \ \mathrm {[J / \left( kg\cdot K\right) ]} \ \),密度\( \ \rho =1.00\times 10^{3} \ \mathrm {[kg / m^{3}]} \ \)であることから,ワンポイント解説「4.水の温度上昇と必要なエネルギーの関係」より,
\[
\begin{eqnarray}
Q &=&\rho Vc \left( T_{2}-T_{1}\right) \\[ 5pt ]
T_{2}-T_{1} &=&\frac {Q}{\rho Vc} \\[ 5pt ]
T_{2} &=&\frac {Q}{\rho Vc}+T_{1} \\[ 5pt ]
&=&\frac {97.2\times 10^{6}}{1.00\times 10^{3}\times 0.370\times 4.18\times 10^{3}}+20.0 \\[ 5pt ]
&≒&82.8 \ \mathrm {[℃]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは