Contents
【問題】
【難易度】★★★★☆(やや難しい)
三相誘導電動機について,次の(a)及び(b)に答えよ。
(a) 一次側に換算した二次巻線の抵抗\( \ {r_{2}}^{\prime } \ \)と滑り\( \ s \ \)の比\( \ \displaystyle \frac {{r_{2}}^{\prime }}{s} \ \)が,他の定数(一次巻線の抵抗\( \ r_{1} \ \),一次巻線のリアクタンス\( \ x_{1} \ \),一次側に換算した二次巻線のリアクタンス\( \ {x_{2}}^{\prime } \ \))に比べて十分に大きくなるように設計された誘導電動機がある。この電動機を電圧\( \ V \ \)の電源に接続して運転したとき,この電動機のトルク\( \ T \ \)と滑り\( \ s \ \),電圧\( \ V \ \)の関係を表す近似式として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,\( \ k \ \)は定数である。
(1) \( \ \displaystyle T=\frac {k}{Vs} \ \) (2) \( \ \displaystyle T=\frac {k}{V^{2}s} \ \) (3) \( \ \displaystyle T=\frac {kV^{2}}{s} \ \)
(4) \( \ T=kV^{2}s \ \) (5) \( \ T=kVs \ \)
(b) 上記(a)で示された条件で設計された定格電圧\( \ 220 \ \mathrm {V} \ \),同期速度\( \ 1 \ 200 \ \mathrm {{min}^{-1}} \ \)の三相誘導電動機がある。この電動機を電圧\( \ 220 \ \mathrm {V} \ \)の電源に接続して,一定トルクの負荷で運転すると,\( \ 1 \ 140 \ \mathrm {{min}^{-1}} \ \)の回転速度で回転する。この電動機に供給する電源電圧を\( \ 200 \ \mathrm {V} \ \)に下げたときの電動機の回転速度\( \ \mathrm {[{min}^{-1}]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,電源電圧を下げたとき,負荷トルクと二次抵抗は変化しないものとする。
(1) \( \ 1 \ 150 \ \) (2) \( \ 1 \ 127 \ \) (3) \( \ 1 \ 113 \ \) (4) \( \ 1 \ 091 \ \) (5) \( \ 1 \ 000 \ \)
【ワンポイント解説】
三相誘導電動機のトルクと滑り,電圧の関係を考える問題です。
設問(a)の導出はどちらかというと知識を問う問題として出題され,導出できる受験生の方が少ない内容かと思いますが,解説では定量的に導出しています。計算の得意不得意,暗記の得意不得意,等あると思いますので,ご自身に合う方法を選択して下さい。
本問は平成17年問15からの再出題となります。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。

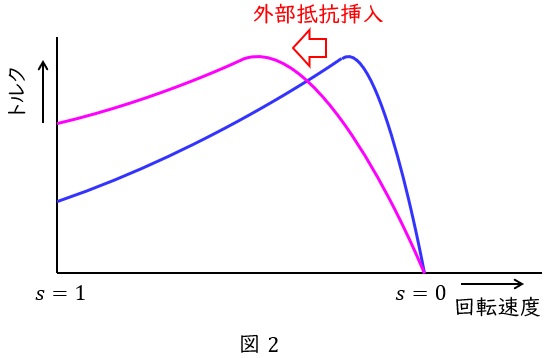
4.巻線形誘導電動機のトルクの比例推移
三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T &=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ 1≫s \ \)の時,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)以外の抵抗やリアクタンスは無視できるので,
\[
\begin{eqnarray}
T &≃& \frac {3V^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
となり,トルクに対する変数は可変抵抗(外部抵抗が挿入可能)である二次抵抗\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)と滑り\( \ s \ \)のみであり,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)を一定とすると,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(a)解答:(4)
図1のような誘導電動機の\( \ \mathrm {L} \ \)形等価回路における二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{2} &=& 3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
&=& 3\frac {r_{2}^{\prime }}{s}\left\{ \frac {V}{\sqrt { \left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}\right\} ^{2} \\[ 5pt ]
&=& \frac {3V^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,同期角速度を\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)とすると,
\[
\begin{eqnarray}
T &=& \frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=& \frac {P_{2}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=& \frac {P_{2} }{\omega _{\mathrm {s}} } \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\( \ \displaystyle \frac {r_{2}^{\prime }}{s}≫r_{1} , x_{1}, {x_{2}}^{\prime } \ \)であるので,
\[
\begin{eqnarray}
T &≃& \frac {1}{\omega _{\mathrm {s}}}\frac {3V^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( \displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}} \\[ 5pt ]
&=&\frac {3V^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
&=&\frac {3}{\omega _{\mathrm {s}}r_{2}^{\prime }}V^{2}s \\[ 5pt ]
&=&kV^{2}s \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(2)
電圧\( \ V=220 \ \mathrm {[V]} \ \),同期速度\( \ N_{\mathrm {s}}=1 \ 200 \ \mathrm {[{min}^{-1}]} \ \),回転速度\( \ N=1 \ 140 \ \mathrm {[{min}^{-1}]} \ \)のときの滑り\( \ s \ \)は,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {1 \ 200-1 \ 140}{1 \ 200} \\[ 5pt ]
&=&0.05 \\[ 5pt ]
\end{eqnarray}
\]
であり,(a)解答式より,一定トルクで\( \ V^{\prime }=200 \ \mathrm {[V]} \ \)のときの滑り\( \ s^{\prime } \ \)は,
\[
\begin{eqnarray}
kV^{2}s &=& k{V^{\prime }}^{2}s^{\prime } \\[ 5pt ]
V^{2}s &=& {V^{\prime }}^{2}s^{\prime } \\[ 5pt ]
s^{\prime }&=&\left( \frac {V}{V^{\prime }}\right) ^{2}s \\[ 5pt ]
&=&\left( \frac {220}{200}\right) ^{2}\times 0.05 \\[ 5pt ]
&=&0.060 \ 5 \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,このときの回転速度\( \ N^{\prime } \ \mathrm {[{min}^{-1}]} \ \)は,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,
\[
\begin{eqnarray}
N^{\prime }&=&\left( 1-s^{\prime } \right) N_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-0.060 \ 5 \right)\times 1 \ 200 \\[ 5pt ]
&≒&1 \ 127 \ \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは