《理論》〈電磁気〉[H18:問4]コイルの自己インダクタンスの導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

巻数\( \ N=10 \ \)のコイルを流れる電流が\( \ 0.1 \ \)秒間に\( \ 0.6 \ \mathrm {[A]} \ \)の割合で変化しているとき，コイルを貫く磁束が\( \ 0.4 \ \)秒間に\( \ 1.2 \ \mathrm {[mWb]} \ \)の割合で変化した。このコイルの自己インダクタンス\( \ L\ \mathrm {[mH]} \ \)の値として，正しいのは次のうちどれか。

ただし，コイルの漏れ磁束は無視できるものとする。

　(1)　\( \ 0.5 \ \)　　(2)　\( \ 2.5 \ \)　　(3)　\( \ 5 \ \)　　(4)　\( \ 10 \ \)　　(5)　\( \ 20 \ \)

【ワンポイント解説】

電流変化や磁束変化の条件からコイルの自己インダクタンスを求める問題です。
ファラデーの電磁誘導の公式を覚えていればあとは数値を代入するだけの問題なので，電験としてはかなり取り組みやすい問題と言えます。
このような問題を確実に得点できるようにしましょう。

1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)
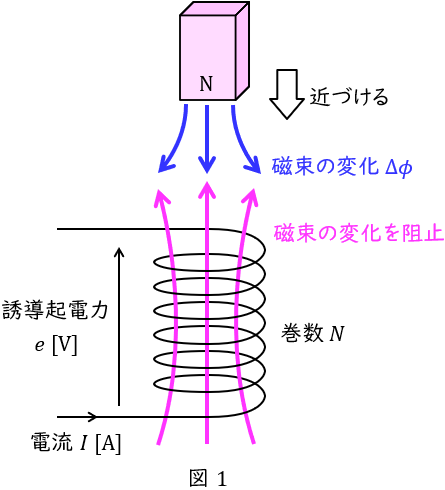
図1に示すように，巻数\( \ N \ \)のコイルを貫通する磁束\( \ \phi \ \mathrm {[Wb]} \ \)があるとき，ファラデーの電磁誘導の法則より，コイルに発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は，磁束の時間変化\( \ \displaystyle \frac {\Delta \phi }{\Delta t} \ \)に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\Delta \phi }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。一方，電流変化\( \ \Delta I \ \mathrm {[A]} \ \)を考える場合，
\[
\begin{eqnarray}
e&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，\( \ L \ \mathrm {[H]}\ \)を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\Delta \phi }{\Delta t}&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

解答：(3)
ファラデーの電磁誘導の法則に\( \ N=10 \ \)，\( \ \Delta t_{1}=0.1 \ \mathrm {[s]} \ \)，\( \ \Delta I =0.6 \ \mathrm {[A]} \ \)，\( \ \Delta t_{2}=0.4 \ \mathrm {[s]} \ \)，\( \ \Delta \phi =1.2\times 10^{-3} \ \mathrm {[Wb]} \ \)を代入すると，ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)」の通り，
\[
\begin{eqnarray}
e=−L\frac {\Delta I }{\Delta t_{1}}&=&−N\frac {\Delta \phi }{\Delta t_{2}} \\[ 5pt ] −L\times \frac {0.6}{0.1}&=&−10\times \frac {1.2\times 10^{-3}}{0.4} \\[ 5pt ] −6L&=&−30\times 10^{-3} \\[ 5pt ] L&=&5\times 10^{-3} \ \mathrm {[H]}　→　5 \ \mathrm {[mH]} \\[ 5pt ] \end{eqnarray}
\] と求められる。