《理論》〈直流回廊〉[H18:問5]内部抵抗を含む電池の起電力の導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

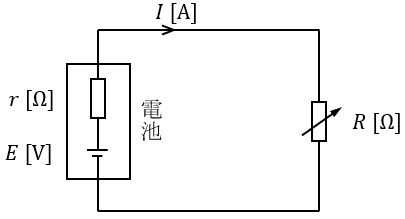
図のように，内部抵抗\( \ r \ \mathrm {[\Omega ]} \ \)，起電力\( \ E \ \mathrm {[V]} \ \)の電池に抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の可変抵抗器を接続した回路がある。\( \ R=2.25 \ \mathrm {[\Omega ]} \ \)にしたとき，回路を流れる電流は\( \ I=3 \ \mathrm {[A]} \ \)であった。次に，\( \ R=3.45 \ \mathrm {[\Omega ]} \ \)にしたとき，回路を流れる電流は\( \ I=2 \ \mathrm {[A]} \ \)となった。この電池の起電力\( \ E \ \mathrm {[V]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ 6.75 \ \)　　(2)　\( \ 6.90 \ \)　　(3)　\( \ 7.05 \ \)　　(4)　\( \ 7.20 \ \)　　(5)　\( \ 9.30 \ \)

【ワンポイント解説】

可変抵抗器の抵抗値を変化したときの電流値の変化から内部抵抗を含む電池の起電力を求める問題です。
キルヒホッフの法則や合成抵抗等の基本公式を利用すれば解くことができます。本問は確実に得点しておきたい問題です。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則（電流則）
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

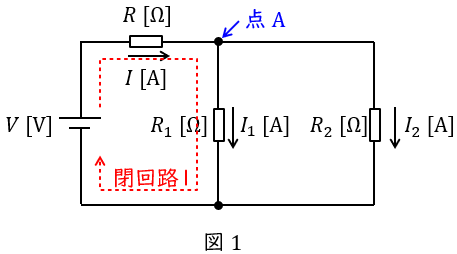
　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則（電圧則）
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

【解答】

解答：(4)
キルヒホッフの法則の電圧則より，回路方程式は，
\[
\begin{eqnarray}
E&=&rI+RI \\[ 5pt ] \end{eqnarray}
\] であり，\( \ R=2.25 \ \mathrm {[\Omega ]} \ \)のとき\( \ I=3 \ \mathrm {[A]} \ \)，\( \ R=3.45 \ \mathrm {[\Omega ]} \ \)のとき\( \ I=2 \ \mathrm {[A]} \ \)であるから，
\[
\begin{eqnarray}
E&=&r\times 3+2.25\times 3 \\[ 5pt ] &=&3r+6.75　・・・・・・・・・・・・・・・　① \\[ 5pt ] E&=&r\times 2+3.45\times 2 \\[ 5pt ] &=&2r+6.90　・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。\( \ ①-② \ \)より，
\[
\begin{eqnarray}
0&=&r-0.15 \\[ 5pt ] r&=&0.15 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，これを\( \ ① \ \)に代入すれば，
\[
\begin{eqnarray}
E&=&3\times 0.15+6.75 \\[ 5pt ] &=&7.20 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。