《理論》〈電気回路〉[H20:問6]スイッチ切換時の電流値からの未知の抵抗値の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，抵抗，切換スイッチ\( \ \mathrm {S} \ \)及び電流計を接続した回路がある。この回路に直流電圧\( \ 100 \ \mathrm {[V]} \ \)を加えた状態で，図のようにスイッチ\( \ \mathrm {S} \ \)を開いたとき電流計の指示値は\( \ 2.0 \ \mathrm {[A]} \ \)であった。また，スイッチ\( \ \mathrm {S} \ \)を①側に閉じたとき電流計の指示値は\( \ 2.5 \ \mathrm {[A]} \ \)，スイッチ\( \ \mathrm {S} \ \)を②側に閉じたとき電流計の指示値は\( \ 5.0 \ \mathrm {[A]} \ \)であった。このとき，抵抗\( \ r \ \mathrm {[\Omega ]} \ \)の値として，正しいのは次のうちどれか。

ただし，電流計の内部抵抗は無視できるものとし，測定誤差はないものとする。

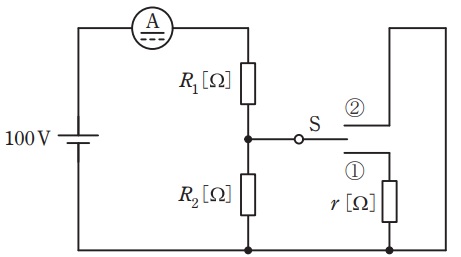
　(1)　\( \ 20 \ \)　　(2)　\( \ 30 \ \)　　(3)　\( \ 40 \ \)　　(4)　\( \ 50 \ \)　　(5)　\( \ 60 \ \)　　

【ワンポイント解説】

スイッチを切り換えた時の電流値の変化から，各抵抗値を求める問題です。
少し手間かもしれませんが，解答のようにスイッチを切り換えた各条件の回路図を描くと間違えにくいかと思います。一つずつ丁寧に計算していくようにしましょう。

1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

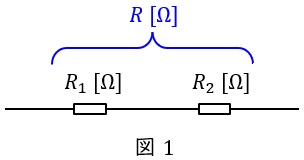
①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

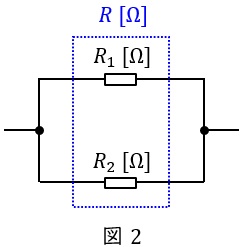
②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
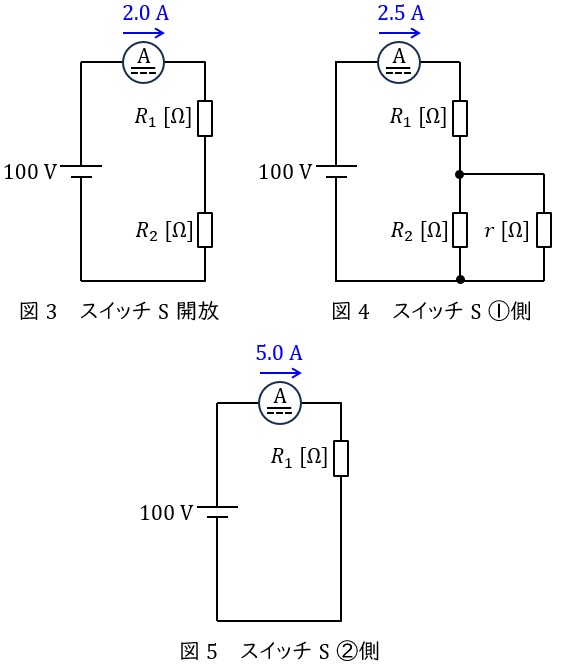
題意の条件に沿って，スイッチが開放時，①側，②側の時の各回路図を描くと図3～図5の通りとなる。

図5より，\( \ R_{1} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{1}&=&\frac {100}{5.0} \\[ 5pt ] &=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，これと図3より，
\[
\begin{eqnarray}
R_{1}+R_{2}&=&\frac {100}{2.0} \\[ 5pt ] 20+R_{2}&=&50 \\[ 5pt ] R_{2}&=&30 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，図4の合成抵抗を求める式より，
\[
\begin{eqnarray}
R_{1}+\frac {R_{2}r}{R_{2}+r}&=&\frac {100}{2.5} \\[ 5pt ] 20+\frac {30r}{30+r}&=&40 \\[ 5pt ] \frac {30r}{30+r}&=&20 \\[ 5pt ] 30r&=&20\left( 30+r\right) \\[ 5pt ] 30r&=&600 +20r \\[ 5pt ] 10r&=&600 \\[ 5pt ] r&=&60 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。