《理論》〈電子理論〉[H21:問13]ソース接地のFET増幅器の静特性に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

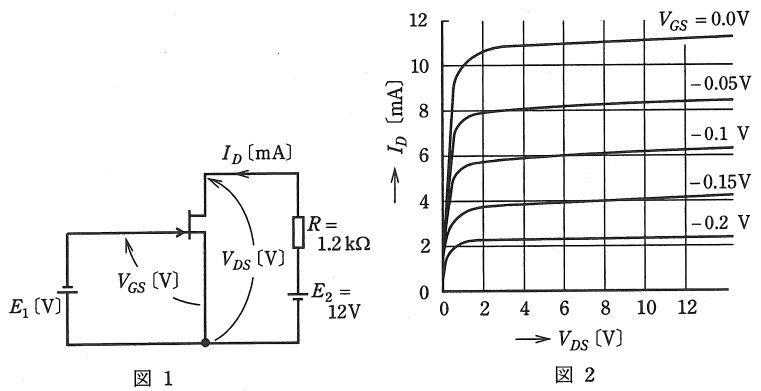
図1にソース接地の\( \ \mathrm {FET} \ \)増幅器の静特性に注目した回路を示す。この回路の\( \ \mathrm {FET} \ \)のドレーン－ソース間電圧\( \ V_{DS} \ \)とドレーン電流\( \ I_{D} \ \)の特性は，図2に示す。図1の回路において，ゲート－ソース間電圧\( \ V_{GS}=-0.1 \ \mathrm {[V]} \ \)のとき，ドレーン－ソース間電圧\( \ V_{DS} \ \mathrm {[V]} \ \)，ドレーン電流\( \ I_{D} \ \mathrm {[mA]} \ \)の値として，最も近いものを組み合わせたのは次のうちどれか。

ただし，直流電源電圧\( \ E_{2}=12 \ \mathrm {[V]} \ \)，負荷抵抗\( \ R=1.2 \ \mathrm {[k\Omega ]} \ \)とする。

\[
\begin{array}{ccc}
& V_{DS} & I_{D} \\
\hline
(1) & 　0.8　 & 　5.0　 \\
\hline
(2) & 　3.0　 & 　5.8　 \\
\hline
(3) & 　4.2　 & 　6.5　 \\
\hline
(4) & 　4.8　 & 　6.0　 \\
\hline
(5) & 　12　 & 　8.4　 \\
\hline
\end{array}
\]

【ワンポイント解説】

\( \ \mathrm {FET} \ \)増幅器の静特性から動作点を求める問題です。
このような静特性の問題はパターンがほぼ決まっており，特別な公式を必要としません。また多くの受験生が勉強しない分野でもあるので，ぜひ得点源にできるようにしましょう。

【解答】

解答：(4)
図1-1に示す閉回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
E_{2}-RI_{D} &=&V_{DS} \\[ 5pt ] RI_{D} &=&E_{2}-V_{DS} \\[ 5pt ] I_{D} &=&\frac {E_{2}-V_{DS}}{R} \\[ 5pt ] &=&\frac {12-V_{DS}}{1.2\times 10^{3}} \\[ 5pt ] \end{eqnarray}
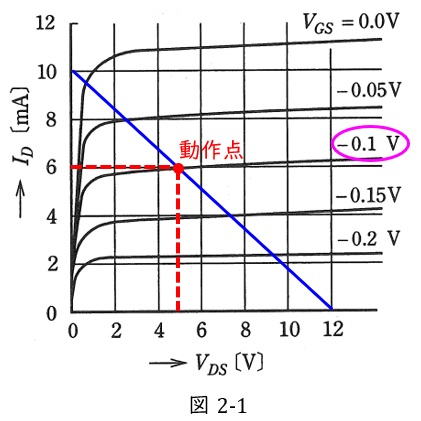
\] となり，\( \ V_{DS}=0 \ \mathrm {[V]} \ \)のとき\( \ I_{D}=10\times 10^{-3} \ \mathrm {[A]} =10 \ \mathrm {[mA]} \ \)，\( \ V_{DS}=12 \ \mathrm {[V]} \ \)のとき\( \ I_{D}=0 \ \mathrm {[A]} \ \)であることから，\( \ I_{D} \ \)と\( \ V_{DS} \ \)の関係は図2-1に示すような直線となる。

ここで，\( \ V_{GS}=-0.1 \ \mathrm {[V]} \ \)であることから，動作点は図2-1に示す通りとなり，このときの\( \ V_{DS}=4.8 \ \mathrm {[V]} \ \)と\( \ I_{D}=6 \ \mathrm {[mA]} \ \)が読み取れる。