Contents
【問題】
【難易度】★★★☆☆(普通)
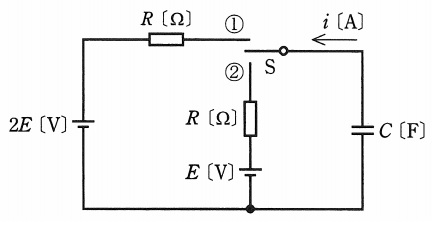
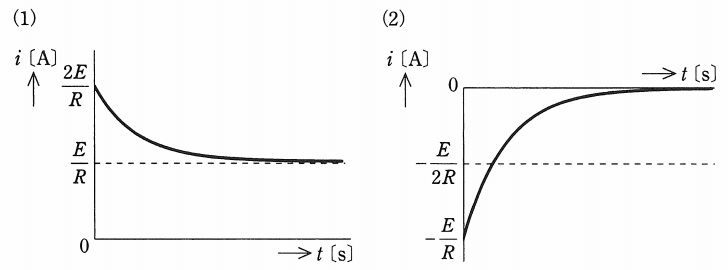
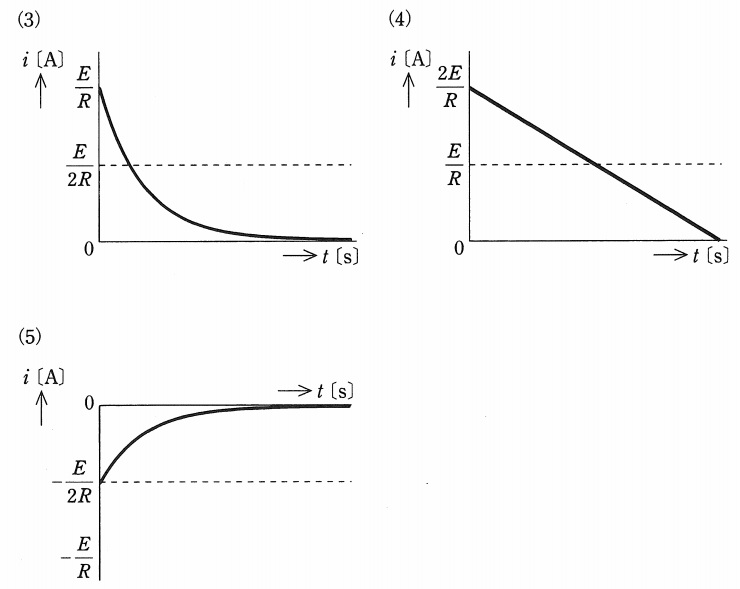
図のように,\( \ 2 \ \)種類の直流電源,\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサ及びスイッチ\( \ \mathrm {S} \ \)からなる回路がある。この回路において,スイッチ\( \ \mathrm {S} \ \)を①側に閉じて回路が定常状態に達した後に,時刻\( \ t=0 \ \mathrm {[s]} \ \)でスイッチ\( \ \mathrm {S} \ \)を①側から②側に切り換えた。②側へ切り換え以降の,コンデンサから流れ出る電流\( \ i \ \mathrm {[A]} \ \)の時間変化を示す図として,正しいものを次の(1)~(5)のうちから一つ選べ。
【ワンポイント解説】
一般的な過渡現象の内容に電源の切換えを組み合わせた問題です。
\( \ 3 \ \)種では微分方程式を使ったような計算問題は出題されないので,本問のような複雑に見える問題でも,スイッチを切り換えた直後(過渡状態)とスイッチを切り換えて十分時間が経った状態(定常状態)をしっかりと理解しておけば解くことが可能です。
1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって,リアクトルに電圧を印加した瞬間はほとんど電流は流れないので,開放として考えます。
② 定常状態
電圧を印加して十分時間が経過した後は,リアクトルの抵抗はほぼ零になります。したがって,短絡として考えます。
2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので,電流がものすごく流れやすい状態,すなわち短絡として考えます。
※ 本問では\( \ t=0 \ \)で電荷が蓄えられているので少し変わります。
② 定常状態
コンデンサに十分に電荷が蓄えられているので,電流をこれ以上蓄えようとしない,すなわち開放として考えます。
【解答】
解答:(3)
スイッチ\( \ \mathrm {S} \ \)を①側に閉じて回路が定常状態に達した時の回路は図1のようになる。
図1において,コンデンサ\( \ C \ \)は開放状態と考えられるので,回路には電流は流れず,電源の電圧\( \ 2E \ \mathrm {[V]} \ \)はすべてコンデンサにかかることになる。

スイッチ\( \ \mathrm {S} \ \)を①側から②側に切り換えた直後は図2のようになり,コンデンサの電圧は\( \ 2E \ \mathrm {[V]} \ \)であるため,キルヒホッフの法則より,
\[
\begin{eqnarray}
2E-E &=&Ri \\[ 5pt ]
i&=&\frac {E}{R} \\[ 5pt ]
\end{eqnarray}
\]
の電流が流れる。
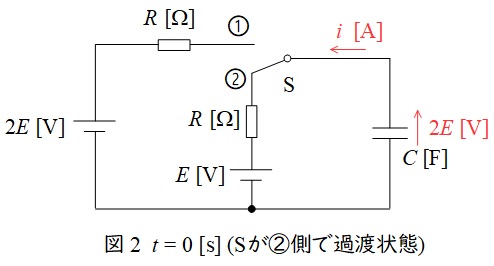
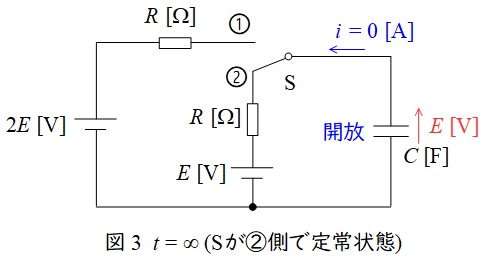
スイッチ\( \ \mathrm {S} \ \)を①側から②側に切り換え十分時間が経過したときの回路は図3のようになり,コンデンサ\( \ C \ \)は開放状態となるので,回路に電流は流れない。
以上の条件を満たすのは(3)のグラフとなる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは