《理論》〈電磁気〉[H23:問2]平行平板コンデンサの静電容量と静電エネルギーに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

直流電圧\( \ 1000 \ \mathrm {[V]} \ \)の電源で充電された静電容量\( \ 8 \ \mathrm {[\mu F]} \ \)の平行平板コンデンサがある。コンデンサを電源から外した後に電荷を保持したままコンデンサの電極間距離を最初の距離の\( \ \displaystyle \frac {1}{2} \ \)に縮めたとき，静電容量\( \ \mathrm {[\mu F]} \ \)と静電エネルギー\( \ \mathrm {[J]} \ \)の値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& 　静電容量　 & 　静電エネルギー　 \\
\hline
(1) & 　16　 & 　4　 \\
\hline
(2) & 　16　 & 　2　 \\
\hline
(3) & 　16　 & 　8　 \\
\hline
(4) & 　4　 & 　4　 \\
\hline
(5) & 　4　 & 　2　 \\
\hline
\end{array}
\]

【ワンポイント解説】

毎年のように出題される平行平板コンデンサに関する問題です。
本問で扱う公式は，いずれも最重要の公式なので，確実に理解しておくようにしましょう。
類題が平成29年問2にも出題されているので，合わせて確認しておきましょう。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量\( \ C \ \)
平板間の誘電率を\( \ \varepsilon \ \)，平板の面積を\( \ S \ \)，平板間の間隔を\( \ d \ \)とすると，静電容量\( \ C \ \)は，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon S}{d} \\[ 5pt ] \end{eqnarray}
\] で求められます。

3.平行平板コンデンサの静電エネルギー\( \ W \ \)
平行平板コンデンサの静電エネルギー\( \ W \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
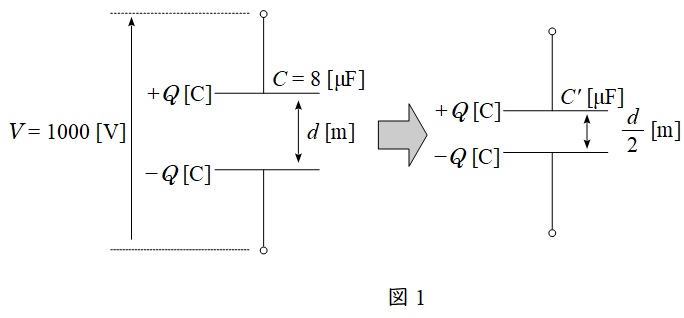
問題に沿って図を描くと図1のようになる。
図1左において，コンデンサに蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] &=&8\times 10^{-6}\times 1000 \\[ 5pt ] &=&8\times 10^{-3} \ \mathrm {[C]}\\[ 5pt ] \end{eqnarray}
\] である。ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り，コンデンサの静電容量は電極間距離\( \ d \ \)に反比例するので，電極間距離を\( \ \displaystyle \frac {1}{2} \ \)に縮めたときの静電容量\( \ C^{\prime } \ \mathrm {[\mu F]} \ \)は\( \ C=8 \ \mathrm {[\mu F]} \ \)の\( \ 2 \ \)倍となる。したがって，
\[
\begin{eqnarray}
C^{\prime } &=&2C \\[ 5pt ] &=&2\times 8 \\[ 5pt ] &=&16 \ \mathrm {[\mu F]}\\[ 5pt ] \end{eqnarray}
\] と求められる。また，このときの静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，ワンポイント解説「3.平行平板コンデンサの静電エネルギー\( \ W \ \)」の通り，
\[
\begin{eqnarray}
W &=&\frac {Q^{2}}{2C^{\prime }} \\[ 5pt ] &=&\frac {\left( 8\times 10^{-3}\right) ^{2}}{2\times 16\times 10^{-6}} \\[ 5pt ] &=&2 \ \mathrm {[J]}\\[ 5pt ] \end{eqnarray}
\] と求められる。