《理論》〈電子理論〉[H24:問18]ＦＥＴ増幅回路の特性に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

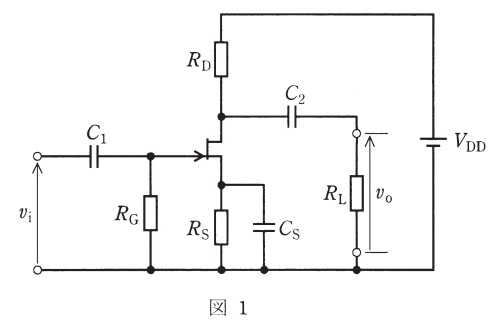
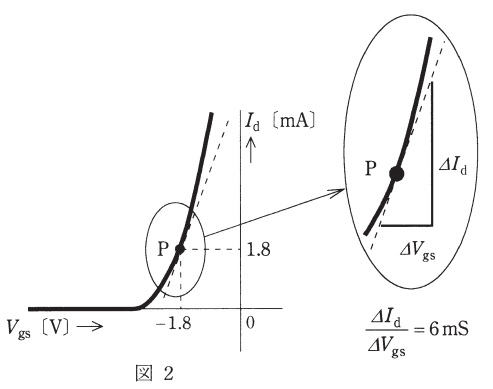
図1は，飽和領域で動作する接合形\( \ \mathrm {FET} \ \)を用いた増幅回路を示し，図中の\( \ v_{\mathrm {i}} \ \)並びに\( \ v_{\mathrm {o}} \ \)はそれぞれ，入力と出力の小信号交流電圧\( \ \mathrm {[V]} \ \)を表す。また，図2は，その増幅回路で使用する\( \ \mathrm {FET} \ \)のゲート－ソース間電圧\( \ V_{\mathrm {gs}} \ \mathrm {[V]} \ \)に対するドレーン電流\( \ I_{\mathrm {d}} \ \mathrm {[mA]} \ \)の特性を示している。抵抗\( \ R_{\mathrm {G}}=1 \ \mathrm {[M\Omega ]} \ \)，\( \ R_{\mathrm {D}}=5 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{\mathrm {L}}=2.5 \ \mathrm {[k\Omega ]} \ \)，直流電源電圧\( \ V_{\mathrm {DD}}=20 \ \mathrm {[V]} \ \)とするとき，次の(a)及び(b)の問に答えよ。

(a)　\( \ \mathrm {FET} \ \)の動作点が図2の点\( \ \mathrm {P} \ \)となる抵抗\( \ R_{\mathrm {S}} \ \mathrm {[k\Omega ]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.1 \ \)　　(2)　\( \ 0.3 \ \)　　(3)　\( \ 0.5 \ \)　　(4)　\( \ 1 \ \)　　(5)　\( \ 3 \ \)

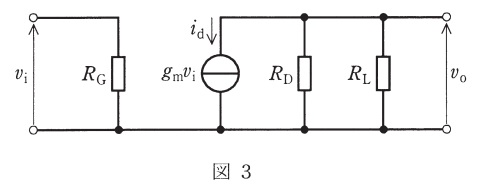
(b)　図2の特性曲線の点\( \ \mathrm {P} \ \)における接線の傾きを読むことで，\( \ \mathrm {FET} \ \)の相互コンダクタンスが\( \ g_{\mathrm {m}}=6 \ \mathrm {[mS]} \ \)であるとわかる。この値を用いて，増幅回路の小信号交流等価回路をかくと図3となる。ここで，コンデンサ\( \ C_{1} \ \)，\( \ C_{2} \ \)，\( \ C_{\mathrm {S}} \ \)のインピーダンスが使用する周波数で十分に小さいときを考えており，\( \ \mathrm {FET} \ \)の出力インピーダンスが\( \ R_{\mathrm {D}} \ \mathrm {[k\Omega ]} \ \)や\( \ R_{\mathrm {L}} \ \mathrm {[k\Omega ]} \ \)より十分大きいとしている。この増幅回路の電圧増幅度\( \ \displaystyle A_{\mathrm {v}}=\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。　

　(1)　\( \ 10 \ \)　　(2)　\( \ 30 \ \)　　(3)　\( \ 50 \ \)　　(4)　\( \ 100 \ \)　　(5)　\( \ 300 \ \)

【ワンポイント解説】

電子回路のやや特殊な問題なので，問題自体はそれほど難しいものではないですが，電験としてはやや難しい部類の問題となると思います。本問は出題されても選択問題となるので，大学等で習得されていない方は飛ばしても構わない問題かもしれません。

【解答】

(a)解答：(4)
図2より動作点\( \ \mathrm {P} \ \)におけるゲート－ソース間電圧\( \ V_{\mathrm {gs}} \ \mathrm {[V]} \ \)及びドレーン電流\( \ I_{\mathrm {d}} \ \mathrm {[mA]} \ \)の大きさは，
\[
\begin{eqnarray}
V_{\mathrm {gs}}&=&-1.8 \ \mathrm {[V]} \\[ 5pt ] I_{\mathrm {d}}&=&1.8 \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
\] である。また，図1において\( \ \mathrm {FET} \ \)の特性より，動作点における入力電流は零であるから，\( \ R_{\mathrm {G}} \ \)には電流が流れないのでゲート電圧は\( \ 0 \ \mathrm {[V]} \ \)である。したがって，ソースの電位\( \ V_{\mathrm {S}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {S}}&=&0-\left( -1.8\right) \\[ 5pt ] &=&1.8 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。また，ドレーン電流はそのままソースに流れるので，\( \ R_{\mathrm {S}} \ \)の大きさは，
\[
\begin{eqnarray}
R_{\mathrm {S}}&=&\frac {V_{\mathrm {S}}}{I_{\mathrm {d}}} \\[ 5pt ] &=&\frac {1.8}{1.8\times 10^{-3}} \\[ 5pt ] &=&1.0\times 10^{3} \ \mathrm {[\Omega ]} \\[ 5pt ] &=&1.0 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
\( \ R_{\mathrm {D}}=5 \ \mathrm {[k\Omega ]} \ \)，\( \ R_{\mathrm {L}}=2.5 \ \mathrm {[k\Omega ]} \ \)の合成抵抗\( \ R_{\mathrm {o}} \ \mathrm {[k\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
R_{\mathrm {o}}&=&\frac {R_{\mathrm {D}}R_{\mathrm {L}}}{R_{\mathrm {D}}+R_{\mathrm {L}}} \\[ 5pt ] &=&\frac {5\times 2.5}{5+2.5} \\[ 5pt ] &≒&1.667 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，出力電圧\( \ v_{\mathrm {o}} \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {o}}&=&-R_{\mathrm {o}}i_{\mathrm {d}} \\[ 5pt ] &=&-R_{\mathrm {o}}g_{\mathrm {m}}v_{\mathrm {i}} \\[ 5pt ] &=&-1.667\times 6\times 10^{-3}\times v_{\mathrm {i}} \\[ 5pt ] &=&-10.0 v_{\mathrm {i}} \\[ 5pt ] \end{eqnarray}
\] となるので，電圧増幅度\( \ \displaystyle A_{\mathrm {v}}=\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)は，
\[
\begin{eqnarray}
\displaystyle A_{\mathrm {v}}&=&\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \\[ 5pt ] &=&\left| -10\right| \\[ 5pt ] &=&10 \\[ 5pt ] \end{eqnarray}
\] と求められる。