《理論》〈電磁気〉[H24:問4]平行直線状導体にかかる力の大きさに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

真空中に，\( \ 2 \ \)本の無限長直線状導体が\( \ 20 \ \mathrm {[cm]} \ \)の間隔で平行に置かれている。一方の導体に\( \ 10 \ \mathrm {[A]} \ \)の直流電流を流しているとき，その導体には\( \ 1 \ \mathrm {[m]} \ \)当たり\( \ 1\times 10^{-6} \ \mathrm {[N]} \ \)の力が働いた。他方の導体に流れている直流電流\( \ I \ \mathrm {[A]} \ \)の大きさとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，真空の透磁率は\( \ \mu _{0}=4\pi \times 10^{-7} \ \mathrm {[H／m]} \ \)である。

　(1)　\( \ 0.1 \ \)　　(2)　\( \ 1 \ \)　　(3)　\( \ 2 \ \)　　(4)　\( \ 5 \ \)　　(5)　\( \ 10 \ \)

【ワンポイント解説】

平行直線状導体間に働く力の大きさに関する問題で，公式を覚えていればあっさりと解けてしまう問題です。ただし，平行直線状導体間に働く力の大きさの公式は丸暗記するのではなく，アンペールの法則とフレミングの左手の法則から自力で導出できるようにしておきましょう。

1.平行直線状導体間に働く力の大きさ
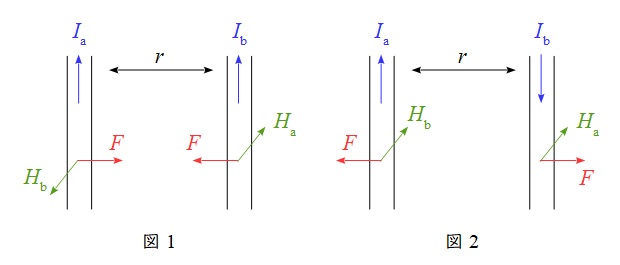
図1のような同方向に電流が流れている場合を考えます。電流\( \ I_{\mathrm {b}} \ \)により発生する電流\( \ I_{\mathrm {a}} \ \)が流れる導体部分の磁界の大きさ\( \ H_{\mathrm {b}} \ \)は，アンペールの法則より，
\[
\begin{eqnarray}
H_{\mathrm {b}}&=&\frac {I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となり，空間の透磁率が\( \ \mu \ \)であるとすると，磁束密度\( \ B_{\mathrm {b}} \ \)は，
\[
\begin{eqnarray}
B_{\mathrm {b}}&=&\mu H_{\mathrm {b}} \\[ 5pt ] &=&\frac {\mu I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。フレミングの左手の法則により，\( \ I_{\mathrm {a}} \ \)の流れる導体にかかる力の大きさは引力となり，その\( \ 1 \ \mathrm {[m]} \ \)あたりの大きさ\( \ F \ \)は，
\[
\begin{eqnarray}
F&=&B_{\mathrm {b}} I_{\mathrm {a}}\times 1 \\[ 5pt ] &=&\frac {\mu I_{\mathrm {a}}I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められます。同様に\( \ I_{\mathrm {b}} \ \)側や図2のような反対向きの場合も求めることができます。

【解答】

解答：(1)
ワンポイント解説「1.平行直線状導体間に働く力の大きさ」の通り，導体間に働く力の大きさは，
\[
\begin{eqnarray}
F&=&\frac {\mu I_{\mathrm {a}}I_{\mathrm {b}}}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] であるので，各値を代入して他方の導体に流れている直流電流を求めると，
\[
\begin{eqnarray}
1\times 10^{-6}&=&\frac {4\pi \times 10^{-7} \times 10 \times I}{2\pi \times 0.2} \\[ 5pt ] I&=&\frac {1\times 10^{-6}\times 2\pi \times 0.2}{4\pi \times 10^{-7} \times 10 } \\[ 5pt ] &=&0.1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。