《理論》〈電気回路〉[H25:問5]キルヒホッフの法則に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と抵抗\( \ R_{\mathrm {x}} \ \mathrm {[\Omega ]} \ \)を並列に接続した回路がある。この回路に直流電圧\( \ V \ \mathrm {[V]} \ \)を加えたところ，電流\( \ I \ \mathrm {[A]} \ \)が流れた。\( \ R_{\mathrm {x}} \ \mathrm {[\Omega ]} \ \)の値を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。

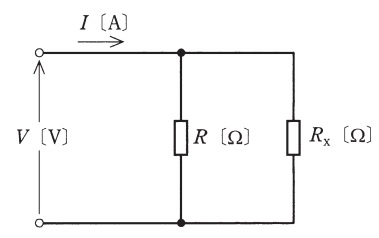
(1)　\( \ \displaystyle \frac {V}{I}+R \ \)　　(2)　\( \ \displaystyle \frac {V}{I}-R \ \)　　(3)　\( \ \displaystyle \frac {R}{\displaystyle \frac {IR}{V}-V} \ \)
(4)　\( \ \displaystyle \frac {V}{\displaystyle \frac {I}{V-R}} \ \)　　(5)　\( \ \displaystyle \frac {VR}{IR-V} \ \)

【ワンポイント解説】

キルヒホッフの法則の第1法則を利用して解く方法，第2法則を利用して解く方法，合成抵抗を求めてオームの法則で解く方法等いろいろな方法があります。答えが合っていればどの方法でも構いません。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

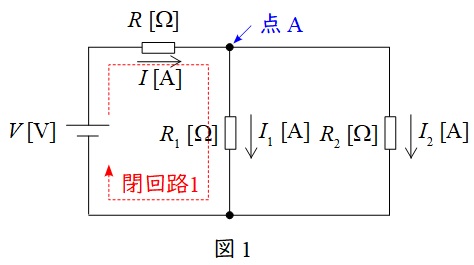
　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

【関連する「電気の神髄」記事】

　　キルヒホッフの法則とその解釈

【解答】

解答：(5)
抵抗\( \ R \ \)及び\( \ R_{\mathrm {x}} \ \)に流れる電流\( \ I_{\mathrm {R}} \ \)及び\( \ I_{\mathrm {Rx}} \ \)は，オームの法則より，
\[
\begin{eqnarray}
I_{\mathrm {R}} &=&\frac {V}{R} \\[ 5pt ] I_{\mathrm {Rx}} &=&\frac {V}{R_{\mathrm {x}}} \\[ 5pt ] \end{eqnarray}
\] であるから，キルヒホッフの第1法則を適用すると，
\[
\begin{eqnarray}
I &=&I_{\mathrm {R}}+I_{\mathrm {Rx}} \\[ 5pt ] &=&\frac {V}{R}+\frac {V}{R_{\mathrm {x}}} \\[ 5pt ] \end{eqnarray}
\] となる。これを\( \ R_{\mathrm {x}} \ \)について整理すると，
\[
\begin{eqnarray}
\frac {V}{R}+\frac {V}{R_{\mathrm {x}}} &=&I \\[ 5pt ] \frac {V}{R_{\mathrm {x}}} &=&I-\frac {V}{R} \\[ 5pt ] \frac {V}{R_{\mathrm {x}}} &=&\frac {IR-V}{R} \\[ 5pt ] \frac {R_{\mathrm {x}}}{V} &=&\frac {R}{IR-V} \\[ 5pt ] R_{\mathrm {x}} &=&\frac {VR}{IR-V} \\[ 5pt ] \end{eqnarray}
\] と求められる。