《理論》〈電気及び電気計測〉[H27:問15]可変抵抗器を含む回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

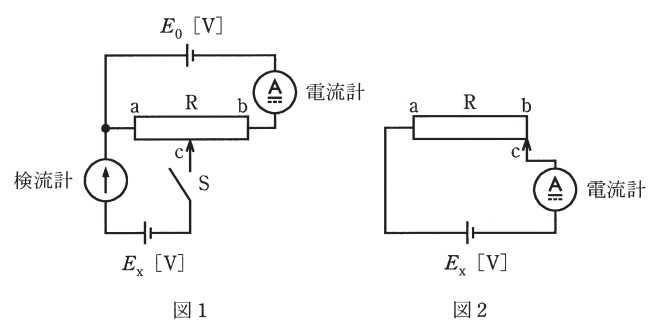
図のように，\(\mathrm {a-b}\)間の長さが\(15 \ \mathrm {cm}\)，最大値が\(30 \ \Omega \)のすべり抵抗器\(\mathrm {R}\)，電流計，検流計，電池\(E_{0} \ \mathrm {[V]}\)，電池\(E_{\mathrm {x}} \ \mathrm {[V]}\)が接続された回路がある。この回路において次のような実験を行った。

実験Ⅰ：図1でスイッチ\(\mathrm {S}\)を開いたとき，電流計は\(200 \ \mathrm {mA}\)を示した。
実験Ⅱ：図1でスイッチ\(\mathrm {S}\)を閉じ，すべり抵抗器\(\mathrm {R}\)の端子\(\mathrm {c}\)を\(\mathrm {b}\)の方向へ移動させて行き，検流計が零を指したとき移動を停止した。このとき，\(\mathrm {a-c}\)間の距離は\(4.5 \ \mathrm {cm}\)であった。
実験Ⅲ：図2に配線を変更したら，電流計の値は\(50 \ \mathrm {mA}\)であった。

次の(a)及び(b)の問に答えよ。

ただし，各計測器の内部抵抗及び接触抵抗は無視できるものとし，また，すべり抵抗器\(\mathrm {R}\)の長さ\(\mathrm {[cm]}\)と抵抗値\(\mathrm {[\Omega]}\)とは比例するものであるとする。

(a)　電池\(E_{\mathrm {x}}\)の起電力の値\(\mathrm {[V]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(1.0\)　　(2)　\(1.2\)　　(3)　\(1.5\)　　(4)　\(1.8\)　　(5)　\(2.0\)

(b)　電池\(E_{\mathrm {x}}\)の内部抵抗の値\(\mathrm {[\Omega]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0.5\)　　(2)　\(2.0\)　　(3)　\(3.5\)　　(4)　\(4.2\)　　(5)　\(6.0\)

【ワンポイント解説】

一見難しそうですが，落ち着いて考えればすべて基本的な回路計算で解くことができます。実験Ⅰ，Ⅱ，Ⅲの各回路がどうなるかを書いて考えましょう。

1.分圧の公式
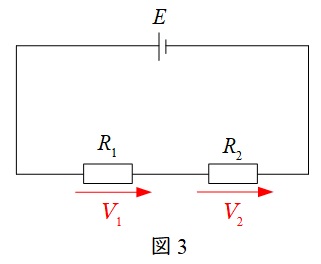
図3のような直列回路がある時，\(R_{1}\)，\(R_{2}\)での電圧降下\(V_{1}\)，\(V_{2}\)は，
\[
\begin{eqnarray}
V_{1}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{2}&=&\frac {R_{2}}{R_{1}+R_{2}}E
\end{eqnarray}
\] で求められます。

【解答】

(a)解答：(4)
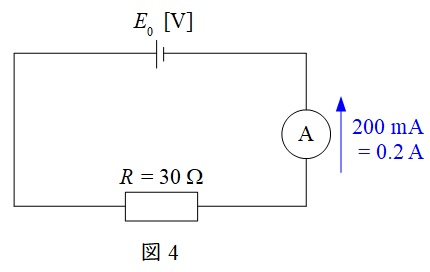
スイッチ\(\mathrm {S}\)は開いているので，実験Ⅰの条件の回路図を描くと図4のようになる。
図4より，電池\(E_{0}\)の電圧は，
\[
\begin{eqnarray}
E_{0}&=&RI_{1} \\[ 5pt ] &=&30\times 0.2 \\[ 5pt ] &=&6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。

次に，実験Ⅱでは\(\mathrm {a-c}\)間の距離は\(4.5 \ \mathrm {cm}\)であるから，その抵抗の大きさ\(R_{\mathrm {ac}}\)は，
\[
\begin{eqnarray}
R_{\mathrm {ac}}&=&30\times \frac {4.5}{15} \\[ 5pt ] &=&9 \ \mathrm {[\Omega ]}
\end{eqnarray}
\] となり，\(\mathrm {c-b}\)間の抵抗の大きさ\(R_{\mathrm {cb}}\)は，
\[
\begin{eqnarray}
R_{\mathrm {cb}}&=&30-9 \\[ 5pt ] &=&21 \ \mathrm {[\Omega ]}
\end{eqnarray}
\] となる。よって，回路図は図5のように描ける。

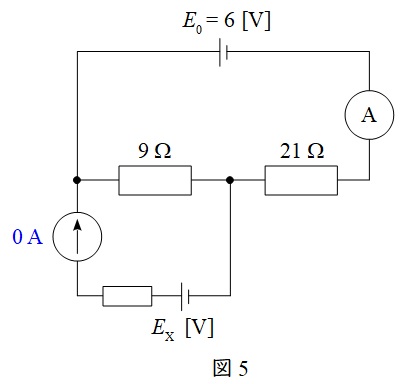
図5において，回路の検流計を流れる電流は零であるので，\(R_{\mathrm {ac}}\)での電圧降下と\(E_{\mathrm {x}}\)の電圧は等しくなければならない。
ワンポイント解説「1.分圧の公式」より，\(R_{\mathrm {ac}}\)での電圧降下\(E_{\mathrm {x}}\)は，
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {9}{9+21}\times 6 \\[ 5pt ] &=&1.8 \ \mathrm {[V]}
\end{eqnarray}
\] と求められる。

(b)解答：(5)
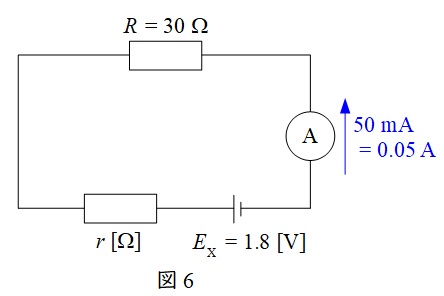
\(E_{\mathrm {x}}\)の内部抵抗の大きさを\(r\)とすると，実験Ⅲにおける回路図は図6のように描ける。
図6より，回路方程式を立てると，内部抵抗の大きさ\(r\)は，
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\left( R+r\right) I_{2} \\[ 5pt ] 1.8&=&\left( 30+r\right) 0.05 \\[ 5pt ] 30+r&=&36 \\[ 5pt ] r&=&6 \ \mathrm {[\Omega ]}
\end{eqnarray}
\] と求められる。