《理論》〈電気回路〉[H27:問4]直流回路の回路計算に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

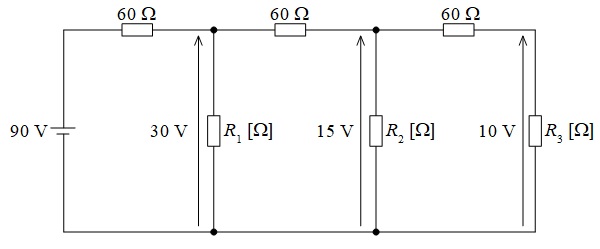
図のような直流回路において，直流電源の電圧が\(90 \ \mathrm {V}\)であるとき，抵抗\(R_{1} \ \mathrm {[\Omega ]}\)，\(R_{2} \ \mathrm {[\Omega ]}\)，\(R_{3} \ \mathrm {[\Omega ]}\)の両端電圧はそれぞれ\(30 \ \mathrm {V}\)，\(15 \ \mathrm {V}\)，\(10 \ \mathrm {V}\)であった。抵抗\(R_{1}\)，\(R_{2}\)，\(R_{3}\)のそれぞれの値\(\mathrm {[\Omega ]}\)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccc}
& 　R_{1}　 & 　R_{2}　 & 　R_{3}　 \\
\hline
(1) & 30 & 90 & 120 \\
\hline
(2) & 80 & 60 & 120 \\
\hline
(3) & 30 & 90 & 30 \\
\hline
(4) & 60 & 60 & 30 \\
\hline
(5) & 40 & 90 & 120 \\
\hline
\end{array}
\]

【ワンポイント解説】

キルヒホッフの法則を理解し，使いこなすことができるかを問う問題となります。キルヒホッフの法則は第一法則，第二法則とも電験受験者であればマスター必須です。

1.キルヒホッフの第一法則
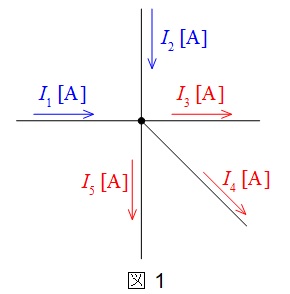
ある点に流れ込む電流の総和と流れ出る電流の総和は等しいという法則です。図1で言えば，
\[
I_{1}+I_{2}=I_{3}+I_{4}+I_{5}
\] となります。

2.キルヒホッフの第二法則
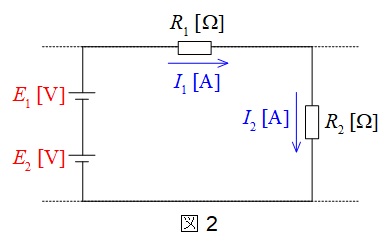
任意の閉回路において，起電力の総和と電圧降下の総和が等しいという法則です。図2で言えば，
\[
E_{1}+E_{2}=R_{1}I_{1}+R_{2}I_{2}
\] となります。

【関連する「電気の神髄」記事】

　　キルヒホッフの法則とその解釈

【解答】

解答：(5)
問題図の抵抗\(R_{1}\)，\(R_{2}\)，\(R_{3}\)に流れる電流を\(I_{1}\)，\(I_{2}\)，\(I_{3}\)とおく。
ワンポイント解説「2.キルヒホッフの第二法則」より，各\(60 \ \Omega \)にかかる電圧は，左から\(60 \ \mathrm {V}\)，\(15 \ \mathrm {V}\)，\(5 \ \mathrm {V}\)となる。

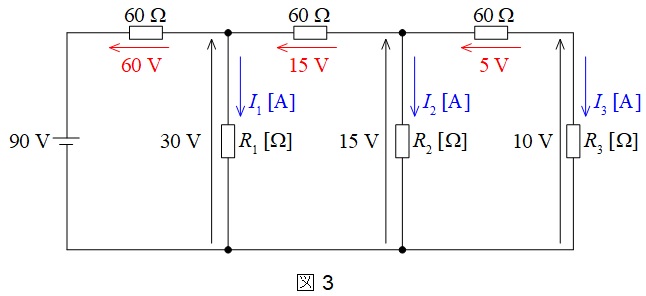
図3において\(I_{3}\)は，隣接する\(60 \ \Omega \)の抵抗に流れる電流と等しいから，
\[
\begin{eqnarray}
I_{3}&=& \frac {5}{60} \\[ 5pt ] &=&\frac {1}{12} \ \mathrm {[A]}
\end{eqnarray}
\] となる。したがって，\(R_{3}\)は，
\[
\begin{eqnarray}
R_{3}&=& \frac {10}{I_{3}} \\[ 5pt ] &=& \frac {10}{\frac {1}{12}} \\[ 5pt ] &=&120 \ [\Omega ] \end{eqnarray}
\] と求められる。
次に真ん中の\(60 \ \Omega \)に流れる電流はキルヒホッフの第一法則より\(I_{2}+I_{3}\)であり，これより\(I_{2}\)の大きさは，
\[
\begin{eqnarray}
I_{2}+I_{3}&=& \frac {15}{60} \\[ 5pt ] I_{2}+\frac {1}{12}&=& \frac {15}{60} \\[ 5pt ] I_{2}&=&\frac {1}{6} \ \mathrm {[A]}
\end{eqnarray}
\] となるので，\(R_{2}\)は，
\[
\begin{eqnarray}
R_{2}&=& \frac {15}{I_{2}} \\[ 5pt ] &=& \frac {15}{\frac {1}{6}} \\[ 5pt ] &=&90 \ [\Omega ] \end{eqnarray}
\] と求められる。
最後に左の\(60 \ \Omega \)に流れる電流はキルヒホッフの第一法則より\(I_{1}+I_{2}+I_{3}\)であり，これより\(I_{1}\)の大きさは，
\[
\begin{eqnarray}
I_{1}+I_{2}+I_{3}&=& \frac {60}{60} \\[ 5pt ] I_{1}+\frac {1}{6}+\frac {1}{12}&=& \frac {60}{60} \\[ 5pt ] I_{1}&=&\frac {3}{4} \ \mathrm {[A]}
\end{eqnarray}
\] となるので，\(R_{1}\)は，
\[
\begin{eqnarray}
R_{1}&=& \frac {30}{I_{1}} \\[ 5pt ] &=& \frac {30}{\frac {3}{4}} \\[ 5pt ] &=&40 \ [\Omega ] \end{eqnarray}
\] と求められる。