《理論》〈電気回路〉[H28:問7]直列接続したコンデンサにかけることができる最大電圧に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

静電容量が\( \ \mathrm {1 \ \mu F} \ \)のコンデンサ\( \ 3 \ \)個を下図のように接続した回路を考える。全てのコンデンサの電圧を\( \ \mathrm {500 \ V} \ \)以下にするために，\( \ \mathrm {a-b} \ \)間に加えることができる最大の電圧\( \ V_{\mathrm {m}} \ \)の値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，各コンデンサの初期電荷は零とする。

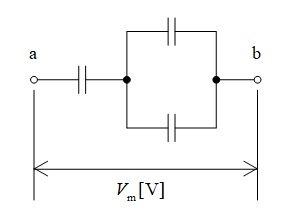
　(1)　\( \ 500 \ \)　　(2)　\( \ 625 \ \)　　(3)　\( \ 750 \ \)　　(4)　\( \ 875 \ \)　　(5)　\( \ 1000 \ \)

【ワンポイント解説】

この問題のポイントはコンデンサが直列接続の場合，蓄えられる電荷が等しいという条件に気が付けるかどうかであると思います。

1.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \)と\( \ C_{2} \ \)のコンデンサがある場合，合成静電容量は下記の通りとなります。
①並列回路の合成静電容量
\[
C=C_{1}+C_{2}
\] ②直列回路の合成静電容量
\[
\frac {1}{C}=\frac {1}{C_{1}}+\frac {1}{C_{2}}　⇔　C=\frac {C_{1}C_{2}}{C_{1}+C_{2}}
\]

【解答】

解答：(3)
並列接続したコンデンサの合成静電容量は，\( \ \mathrm {1 \ \mu F \ + 1 \ \mu F \ = \ 2 \ \mu F \ }\)であるから，問題図は図1のように変換することができる。
ここで，直列接続したコンデンサに蓄えられる電荷は等しいので\(Q\)とおき，各電圧を図1のように定める。

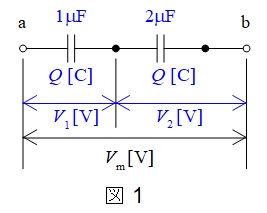
図1より，\( \ V_{1} \ \)と\( \ V_{2} \ \)は，
\[
\begin{eqnarray}
V_{1}&=&\frac {Q}{1\times 10^{-6}}=Q\times 10^{6} \\[ 5pt ] V_{2}&=&\frac {Q}{2\times 10^{-6}}=\frac {Q}{2} \times 10^{6} \\[ 5pt ] \end{eqnarray}
\] となるため，\( \ V_{1}=2 V_{2} \ \)となる。
よって，全てのコンデンサ電圧を\( \ \mathrm {500 \ V} \ \)以下にするためには，\( \ V_{1}=\mathrm {500 \ V} \ \)以下となり，\( \ V_{2}=\mathrm {250 \ V} \ \)以下となる。
したがって，加えることができる最大電圧\( \ V_{\mathrm {m}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {m}}&=&V_{1}+V_{2} \\[ 5pt ] &=&500+250 \\[ 5pt ] &=&750 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。