《理論》〈電気回路〉[H29:問6]直流回路の定常状態に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

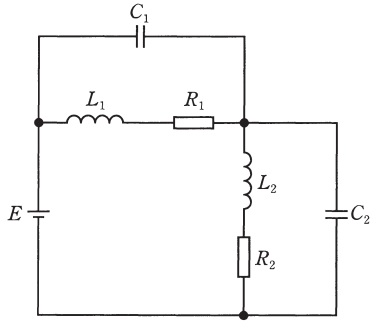
\( \ R_{1}=20 \ \Omega \ \)，\( \ R_{2}=30 \ \Omega \ \)の抵抗，インダクタンス\( \ L_{1}=20 \ \mathrm {mH} \ \)，\( \ L_{2}=40 \ \mathrm {mH} \ \)のコイル及び静電容量\( \ C_{1}=400 \ \mathrm {\mu F} \ \)，\( \ C_{2}=600 \ \mathrm {\mu F} \ \)のコンデンサからなる図のような直並列回路がある。直流電圧\( \ E=100 \ \mathrm {V} \ \)を加えたとき，定常状態において，\( \ L_{1} \ \)，\( \ L_{2} \ \)，\( \ C_{1} \ \)及び\( \ C_{2} \ \)に蓄えられるエネルギーの総和の値\( \ \left[ \mathrm {J}\right] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　　

　(1)　\(0.12\)　　(2)　\(1.20\)　　(3)　\(1.32\)　　(4)　\(1.40\)　　(5)　\(1.52\)

【ワンポイント解説】

定常状態における各インピーダンスの特性を確認する問題です。定常状態とは，接続して十分時間が経ち回路として安定した状態のことです。直流回路では，コンデンサには電流は流れないので，交流回路と勘違いしないようにしましょう。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

3.自己インダクタンス\( \ L \ \)と蓄積される電磁エネルギー\( \ W \ \)の関係式
自己インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルに電流\( \ I \ \mathrm {[A]} \ \)を流し，十分時間が経過した時にコイルに蓄えられるエネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}LI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

4.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)が加わっているとすると，十分時間が経過した時にコンデンサに蓄えられる静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
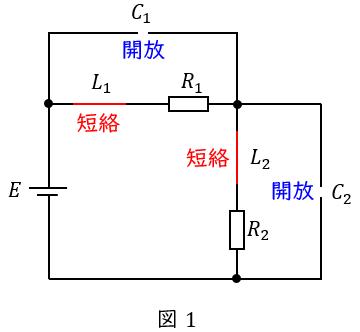
ワンポイント解説「1.過渡現象におけるリアクトルの過渡状態と定常状態」及び「2.過渡現象におけるコンデンサの過渡状態と定常状態」の通り，定常状態においてはコイルは短絡，コンデンサは開放と考えれば良いので，回路は図1のようになる。
したがって，\( \ L_{1} \ \)及び\( \ L_{2} \ \)に流れる電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I &=&\frac {E}{R_{1}+R_{2}} \\[ 5pt ] &=&\frac {100}{20+30} \\[ 5pt ] &=&2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ C_{1} \ \)及び\( \ C_{2} \ \)に加わる電圧\( \ V_{1} \ \mathrm {[V]} \ \)及び\( \ V_{2} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{1} &=&R_{1}I \\[ 5pt ] &=&20\times 2 \\[ 5pt ] &=&40 \ \mathrm {[V]} \\[ 5pt ] V_{2} &=&R_{2}I \\[ 5pt ] &=&30\times 2 \\[ 5pt ] &=&60 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，\( \ L_{1} \ \)，\( \ L_{2} \ \)，\( \ C_{1} \ \)及び\( \ C_{2} \ \)に蓄えられるエネルギーの総和\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}L_{1}I^{2}+\frac {1}{2}L_{2}I^{2}+\frac {1}{2}C_{1}V_{1}^{2}+\frac {1}{2}C_{2}V_{2}^{2} \\[ 5pt ] &=&\frac {1}{2}\times 20\times 10^{-3}\times 2^{2}+\frac {1}{2}\times 40\times 10^{-3}\times 2^{2}+\frac {1}{2}\times 400\times 10^{-6}\times 40^{2}+\frac {1}{2}\times 600\times 10^{-6}\times 60^{2} \\[ 5pt ] &=&0.04+0.08+0.32+1.08 \\[ 5pt ] &=&1.52 \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] と求められる。