《理論》〈電気回路〉[H30:問9]交流回路の共振現象に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

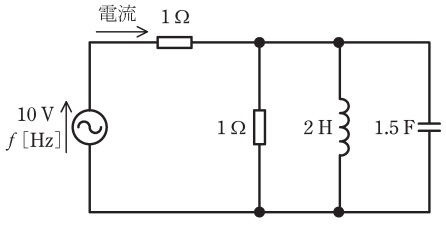
次の文章は，図の回路に関する記述である。

交流電圧源の出力電圧を\(10 \ \mathrm {V}\)に保ちながら周波数\(f \ \mathrm {[Hz]}\)を変化させるとき，交流電圧源の電流の大きさが最小となる周波数は\(\fbox {　 （ア） 　} \ \mathrm {Hz} \ \)である。このとき，この電流の大きさは\(\fbox {　 （イ） 　} \ \mathrm {A} \ \)であり，その位相は電源電圧を基準として\(\fbox {　 （ウ） 　}\)。

ただし，電流の向きは図に示す矢印のとおりとする。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccc}
& （ア） & （イ） & 　　　（ウ）　　　 \\
\hline
(1) & \displaystyle \frac {1}{\sqrt {3}\pi } & 5 & 同相である \\
\hline
(2) & \displaystyle \frac {1}{\sqrt {3}\pi } & 10 & \displaystyle \frac {\pi }{2}\mathrm {rad}だけ進む \\
\hline
(3) & \displaystyle \frac {1}{2\sqrt {3}\pi } & 5 & 同相である \\
\hline
(4) & \displaystyle \frac {1}{2\sqrt {3}\pi } & 10 & \displaystyle \frac {\pi }{2}\mathrm {rad}だけ遅れる \\
\hline
(5) & \displaystyle \frac {1}{2\sqrt {3}\pi } & 5 & \displaystyle \frac {\pi }{2}\mathrm {rad}だけ進む \\
\hline
\end{array}
\]

【ワンポイント解説】

並列回路の共振条件に関する問題です。共振周波数は直列と並列で全く同じ式となりますが，導出方法は直列ではインピーダンス，並列ではアドミタンス（インピーダンスの逆数）で求めるため，全く違うものになります。式の丸暗記ではなく，なぜその共振周波数になるかを理解するようにしましょう。

1.直列回路の共振条件
共振条件は電圧と電流が同位相になる状態で，回路のリアクタンスが零になる状態のことを言います。\(RLC\)直列回路のリアクタンスの共振条件は，角周波数を\(\omega =2\pi f\)とすると，
\[
\begin{eqnarray}
\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C}&=&0 \\[ 5pt ] \mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) &=& 0 \\[ 5pt ] \omega L &=& \frac {1}{\omega C} \\[ 5pt ] \end{eqnarray}
\] の時共振となり，その共振角周波数と共振周波数は，上式を\( \ \omega \ \)について整理すると，
\[
\begin{eqnarray}
\omega ^{2}&=&\frac {1}{LC} \\[ 5pt ] \omega &=&\frac {1}{\sqrt {LC}} \\[ 5pt ] f &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.並列回路の共振条件
共振条件は電圧と電流が同位相になる状態で，回路のサセプタンスが零(リアクタンスが無限大)になる状態のことを言います。\(RLC\)並列回路の共振条件は，角周波数を\(\omega =2\pi f\)とすると，
\[
\begin{eqnarray}
\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L}&=&0 \\[ 5pt ] \mathrm {j}\left( \omega C -\frac {1}{\omega L}\right) &=& 0 \\[ 5pt ] \omega C &=& \frac {1}{\omega L} \\[ 5pt ] \end{eqnarray}
\] の時共振となり，その共振角周波数と共振周波数は，
\[
\begin{eqnarray}
\omega &=&\frac {1}{\sqrt {LC}} \\[ 5pt ] f &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【関連する「電気の神髄」記事】

　　多導体送電線のインダクタンスと等価半径
　　並列共振回路の理論

【解答】

解答：(3)
(ア)
ワンポイント解説「2.並列回路の共振条件」より，共振周波数\(f\)は，
\[
\begin{eqnarray}
f &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] &=&\frac {1}{2\pi \sqrt {2\times 1.5}} \\[ 5pt ] &=&\frac {1}{2\sqrt {3}\pi } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(イ)
共振条件の時，インダクタンスとコンデンサの合成リアクタンスは無限大であるから，電源からの電流はすべて抵抗に流れる。
したがって，その大きさ\(I\)は，
\[
\begin{eqnarray}
I &=&\frac {10}{1+1} \\[ 5pt ] &=&5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(ウ)
問題図の回路において電源からの電流はすべて抵抗に流れるので，電圧と電流は同相となる。