Contents
【問題】
【難易度】★★★★☆(やや難しい)
図1は,飽和領域で動作する接合形\( \ \mathrm {FET} \ \)を用いた増幅回路を示し,図中の\( \ v_{\mathrm {i}} \ \)並びに\( \ v_{\mathrm {o}} \ \)はそれぞれ,入力と出力の小信号交流電圧\( \ \mathrm {[V]} \ \)を表す。また,図2は,その増幅回路で使用する\( \ \mathrm {FET} \ \)のゲート-ソース間電圧\( \ V_{\mathrm {gs}} \ \mathrm {[V]} \ \)に対するドレーン電流\( \ I_{\mathrm {d}} \ \mathrm {[mA]} \ \)の特性を示している。抵抗\( \ R_{\mathrm {G}}=1 \ \mathrm {M\Omega } \ \),\( \ R_{\mathrm {D}}=5 \ \mathrm {k\Omega } \ \),\( \ R_{\mathrm {L}}=2.5 \ \mathrm {k\Omega } \ \),直流電源電圧\( \ V_{\mathrm {DD}}=20 \ \mathrm {V} \ \)とするとき,次の(a)及び(b)の問に答えよ。
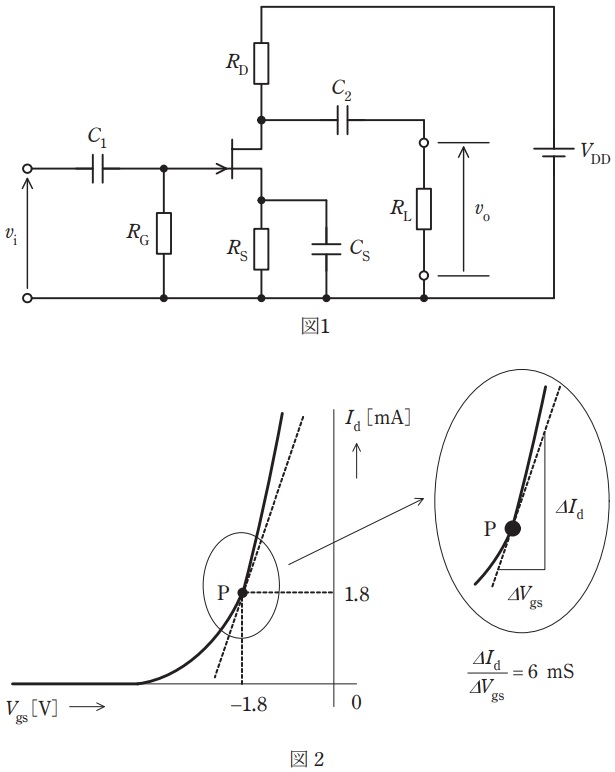
(a) \( \ \mathrm {FET} \ \)の動作点が図2の点\( \ \mathrm {P} \ \)となる抵抗\( \ R_{\mathrm {S}} \ \)の値\( \ \mathrm {[k\Omega ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.1 \ \) (2) \( \ 0.3 \ \) (3) \( \ 0.5 \ \) (4) \( \ 1 \ \) (5) \( \ 3 \ \)
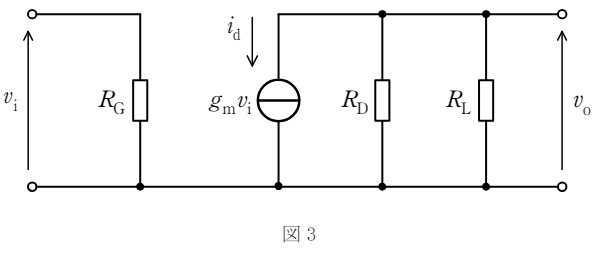
(b) 図2の特性曲線の点\( \ \mathrm {P} \ \)における接線の傾きを読むことで,\( \ \mathrm {FET} \ \)の相互コンダクタンスが\( \ g_{\mathrm {m}}=6 \ \mathrm {mS} \ \)であるとわかる。この値を用いて,増幅回路の小信号交流等価回路をかくと図3となる。ここで,コンデンサ\( \ C_{1} \ \),\( \ C_{2} \ \),\( \ C_{\mathrm {S}} \ \)のインピーダンスが使用する周波数で十分に小さいときを考えており,\( \ \mathrm {FET} \ \)の出力インピーダンスが\( \ R_{\mathrm {D}} \ \mathrm {[k\Omega ]} \ \)や\( \ R_{\mathrm {L}} \ \mathrm {[k\Omega ]} \ \)より十分大きいとしている。
この増幅回路の電圧増幅度\( \ \displaystyle A_{\mathrm {v}}=\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 10 \ \) (2) \( \ 30 \ \) (3) \( \ 50 \ \) (4) \( \ 100 \ \) (5) \( \ 300 \ \)
【ワンポイント解説】
動作する接合形\( \ \mathrm {FET} \ \)を用いた増幅回路の電圧増幅率を求める問題です。
\( \ \mathrm {FET} \ \)はパターンは決まっている問題ですが,電験での出題率は少なく,出題されても選択問題となりますので,効率的な勉強を考えると学習範囲外としても良いかもしれません。
本問は平成24年問18からの再出題となります。
【解答】
(a)解答:(4)
図2より動作点\( \ \mathrm {P} \ \)におけるゲート-ソース間電圧\( \ V_{\mathrm {gs}} \ \mathrm {[V]} \ \)及びドレーン電流\( \ I_{\mathrm {d}} \ \mathrm {[mA]} \ \)の大きさは,
\[
\begin{eqnarray}
V_{\mathrm {gs}}&=&-1.8 \ \mathrm {[V]} \\[ 5pt ]
I_{\mathrm {d}}&=&1.8 \ \mathrm {[mA]} \\[ 5pt ]
\end{eqnarray}
\]
である。また,図1において\( \ \mathrm {FET} \ \)の特性より,動作点における入力電流は零であるから,\( \ R_{\mathrm {G}} \ \)には電流が流れないのでゲート電圧は\( \ 0 \ \mathrm {[V]} \ \)である。したがって,ソースの電位\( \ V_{\mathrm {S}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {S}}&=&0-\left( -1.8\right) \\[ 5pt ]
&=&1.8 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,ドレーン電流はそのままソースに流れるので,\( \ R_{\mathrm {S}} \ \)の大きさは,
\[
\begin{eqnarray}
R_{\mathrm {S}}&=&\frac {V_{\mathrm {S}}}{I_{\mathrm {d}}} \\[ 5pt ]
&=&\frac {1.8}{1.8\times 10^{-3}} \\[ 5pt ]
&=&1.0\times 10^{3} \ \mathrm {[\Omega ]} \\[ 5pt ]
&=&1.0 \ \mathrm {[k\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
\( \ R_{\mathrm {D}}=5 \ \mathrm {[k\Omega ]} \ \),\( \ R_{\mathrm {L}}=2.5 \ \mathrm {[k\Omega ]} \ \)の合成抵抗\( \ R_{\mathrm {o}} \ \mathrm {[k\Omega ]} \ \)の大きさは,
\[
\begin{eqnarray}
R_{\mathrm {o}}&=&\frac {R_{\mathrm {D}}R_{\mathrm {L}}}{R_{\mathrm {D}}+R_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {5\times 2.5}{5+2.5} \\[ 5pt ]
&≒&1.667 \ \mathrm {[k\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,出力電圧\( \ v_{\mathrm {o}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {o}}&=&-R_{\mathrm {o}}i_{\mathrm {d}} \\[ 5pt ]
&=&-R_{\mathrm {o}}g_{\mathrm {m}}v_{\mathrm {i}} \\[ 5pt ]
&=&-1.667\times 6\times 10^{-3}\times v_{\mathrm {i}} \\[ 5pt ]
&=&-10.0 v_{\mathrm {i}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電圧増幅度\( \ \displaystyle A_{\mathrm {v}}=\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \ \)は,
\[
\begin{eqnarray}
\displaystyle A_{\mathrm {v}}&=&\left| \frac {v_{\mathrm {o}}}{v_{\mathrm {i}}}\right| \\[ 5pt ]
&=&\left| -10\right| \\[ 5pt ]
&=&10 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは