《理論》〈電気及び電子計測〉[R2:問16]直列接続した直流電圧計の測定可能電圧に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

最大目盛\( \ 150 \ \mathrm {V} \ \)，内部抵抗\( \ 18 \ \mathrm {k\Omega } \ \)の直流電圧計\( \ \mathrm {V}_{1} \ \)と最大目盛\( \ 300 \ \mathrm {V} \ \)，内部抵抗\( \ 30 \ \mathrm {k\Omega } \ \)の直流電圧計\( \ \mathrm {V}_{2} \ \)の二つの直流電圧計がある。ただし，二つの直流電圧計は直動式指示電気計器を使用し，固有誤差はないものとする。次の(a)及び(b)の問に答えよ。

(a)　二つの直流電圧計を直列に接続して使用したとき，測定できる電圧の最大の値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 150 \ \)　　(2)　\( \ 225 \ \)　　(3)　\( \ 300 \ \)　　(4)　\( \ 400 \ \)　　(5)　\( \ 450 \ \)

(b)　次に，直流電圧\( \ 450 \ \mathrm {V} \ \)の電圧を測定するために，二つの直流電圧計の指示を最大目盛にして測定したい。そのためには，直流電圧計\( \ \fbox {　 （ア） 　} \ \)に，抵抗\( \ \fbox {　 （イ） 　} \ \mathrm {k\Omega } \ \)を\( \ \fbox {　 （ウ） 　} \ \)に接続し，これに直流電圧計\( \ \fbox {　 （エ） 　} \ \)を直列に接続する。このように接続して測定することで，各直流電圧計の指示を最大目盛にして測定をすることができる。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　\mathrm {V}_{1}　 & 　90　 & 　直列　 & 　\mathrm {V}_{2}　 \\
\hline
(2) & 　\mathrm {V}_{1}　 & 　90　 & 　並列　 & 　\mathrm {V}_{2}　 \\
\hline
(3) & 　\mathrm {V}_{2}　 & 　90　 & 　並列　 & 　\mathrm {V}_{1}　 \\
\hline
(4) & 　\mathrm {V}_{1}　 & 　18　 & 　並列　 & 　\mathrm {V}_{2}　 \\
\hline
(5) & 　\mathrm {V}_{2}　 & 　18　 & 　直列　 & 　\mathrm {V}_{1}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

(a)は比較的平易な問題で，(b)が少し考え方に工夫が必要な問題で，B問題としては標準レベルの問題と言えると思います。「倍率器が抵抗を直列に繋げるから・・・」と内容を丸暗記していると，電験では足元をすくわれます。確実に理論を理解した上で解けるようになることが重要かと思います。

1.分圧・分流の法則
①分圧の法則
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
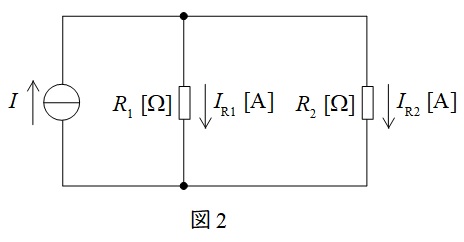
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(4)
ワンポイント解説「1.分圧・分流の法則」の通り，それぞれの電圧計にかかる電圧は，測定電圧を\( \ V \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {1}}&=&\frac {R_{1}}{R_{1}+R_{2}}V \\[ 5pt ] &=&\frac {18\times 10^{3}}{18\times 10^{3}+30\times 10^{3}}V \\[ 5pt ] &=&0.375V \\[ 5pt ] V_{\mathrm {2}}&=&\frac {R_{2}}{R_{1}+R_{2}}V \\[ 5pt ] &=&\frac {30\times 10^{3}}{18\times 10^{3}+30\times 10^{3}}V \\[ 5pt ] &=&0.625V \\[ 5pt ] \end{eqnarray}
\] となるから，\( \ V_{1}=150 \ \mathrm {[V]} \ \)，\( \ V_{2}=300 \ \mathrm {[V]} \ \)を代入すると，それぞれ\( \ V \ \)は，
\[
\begin{eqnarray}
150&=&0.375V \\[ 5pt ] V&=&400 \ \mathrm {[V]} \\[ 5pt ] 300&=&0.625V \\[ 5pt ] V&=&480 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ V_{2} \ \)を上限にとると，\( \ V_{1}=180 \ \mathrm {[V]} \ \)となってしまうので，オーバーレンジとなってしまう。
したがって，測定できる電圧\( \ V \ \)の最大値は\( \ 400 \ \mathrm {V} \ \)と求められる。

(b)解答：(2)
二つの直流電圧計の指示を最大目盛にして測定するとき，それぞれの電圧計に流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)及び\( \ I_{2} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {150}{18\times 10^{3}} \\[ 5pt ] &≒&0.008333 \ \mathrm {[A]} \\[ 5pt ] I_{2}&=&\frac {300}{30\times 10^{3}} \\[ 5pt ] &=&0.01 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。直列に抵抗をつなぐと，測定電圧が小さくなってしまうため，抵抗は並列に繋ぐ必要がある。したがって，電圧計\( \ \mathrm {V}_{1} \ \)に並列に抵抗を接続し，抵抗に
\[
\begin{eqnarray}
I_{2}-I_{1}&=&0.01-0.008333 \\[ 5pt ] &=&0.001667 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] 流すように抵抗値を設定すればよい。したがって，並列抵抗\( \ R \ \mathrm {[k\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
R&=&\frac {150}{0.001667} \\[ 5pt ] &≒&90 \ 000 \ \mathrm {[\Omega]}　→　90 \ \mathrm {[k\Omega]} \\[ 5pt ] \end{eqnarray}
\] と求められる。以上から，条件を満たす解答は(2)となる。