《理論》〈電気回路〉[R4上:問7]合成抵抗値からの未知の抵抗の導出に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図のように，抵抗\( \ 6 \ \)個を接続した回路がある。この回路において，\( \ \mathrm {ab} \ \)端子間の合成抵抗の値が\( \ 0.6 \ \Omega \ \)であった。このとき，抵抗\( \ R_{\mathrm {x}} \ \)の値\( \ [\Omega ] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

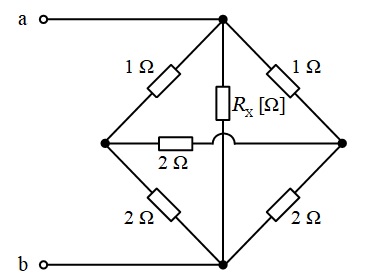
　(1)　\( \ 1.0 \ \)　　(2)　\( \ 1.2 \ \)　　(3)　\( \ 1.5 \ \)　　(4)　\( \ 1.8 \ \)　　(5)　\( \ 2.0 \ \)　　

【ワンポイント解説】

直並列回路の合成抵抗の応用問題です。
このような問題はできるだけ回路を単純化して見やすい形にするとわかりやすくなります。
電験受験生だとこのような問題でも結構正答率は高いので，合格のためには確実に理解しておきたい問題です。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
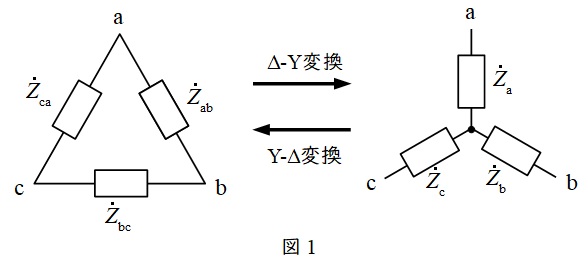
①\( \ \Delta -\mathrm {Y} \ \)変換
図1において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\( \ \mathrm {Y}-\Delta \ \)変換
図1において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\] となります。

【解答】

解答：(1)
問題図の回路を書き換えると図2に示す通りとなる。

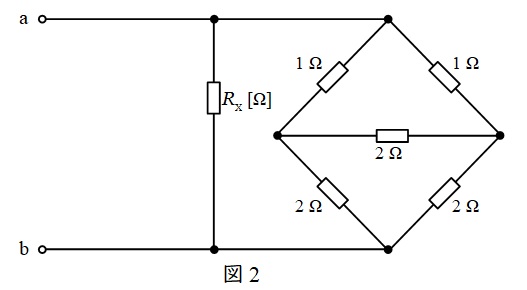
図2の右側の３つの\( \ 2 \ \Omega \ \)の抵抗について，\( \ \Delta -\mathrm {Y} \ \)変換すると，ワンポイント解説「2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り，抵抗値は\( \ \displaystyle \frac {2}{3} \ \Omega \ \)となるから，回路は図3のように書き換えられる。

図3において，\( \ R_{\mathrm {x}} \ \)を除く既知の抵抗の合成抵抗\( \ R \ \)は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R&=&\frac {2}{3}+\frac {\displaystyle \left( \frac {2}{3}+1\right) \left( \frac {2}{3}+1\right) }{\displaystyle \left( \frac {2}{3}+1\right) +\left( \frac {2}{3}+1\right) } \\[ 5pt ] &=&\frac {2}{3}+\frac {\displaystyle \frac {25}{9}}{\displaystyle \frac {10}{3} } \\[ 5pt ] &=&\frac {2}{3}+\frac {5}{6} \\[ 5pt ] &=&\frac {3}{2} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，図4のように書き換えられる。

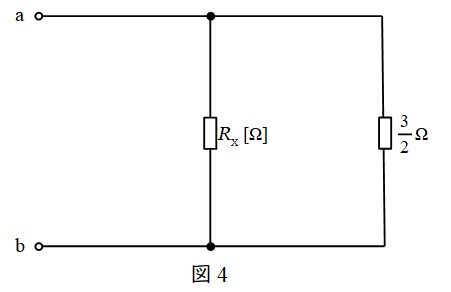
全体の合成抵抗が\( \ 0.6 \ \Omega \ \)であることから，ワンポイント解説「1.合成抵抗」より，
\[
\begin{eqnarray}
\frac {1}{0.6}&=&\frac {1}{R_{\mathrm {x}}}+\frac {1}{R} \\[ 5pt ] \frac {5}{3}&=&\frac {1}{R_{\mathrm {x}}}+\frac {2}{3} \\[ 5pt ] \frac {1}{R_{\mathrm {x}}}&=&1 \\[ 5pt ] R_{\mathrm {x}}&=&1 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※別解として，図2においてブリッジの平衡条件を満たしているので，そこに気が付いた場合には\( \ \Delta -\mathrm {Y} \ \)変換を使用しなくても\( \ 2 \ \Omega \ \)の抵抗を外して解くことが可能です。