《理論》〈電子理論〉[R4下:問13]正弦波を出力している発振回路の発振条件に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図1は，正弦波を出力しているある発振回路の構造を示している。この発振回路の帰還回路の出力端子と増幅回路の入力端子との接続を切り離し，図2のように適当な周波数の正弦波\( \ V_{\mathrm {i}} \ \)を増幅回路に入力すると，次の二つの条件が同時に満たされている。

１．増幅回路の入力電圧\( \ V_{\mathrm {i}} \ \)と帰還回路の出力電圧\( \ V_{\mathrm {f}} \ \)が\( \ \fbox {　 （ア） 　} \ \)である。

２．増幅回路の増幅度\( \ \displaystyle \left| \frac {V_{\mathrm {o}}}{V_{\mathrm {i}}}\right| \ \)を\( \ A \ \)，帰還回路の帰還率\( \ \displaystyle \left| \frac {V_{\mathrm {f}}}{V_{\mathrm {o}}}\right| \ \)を\( \ \beta \ \)と表すとき，\( \ \fbox {　 （イ） 　} \ \)である。

図1で示される発振回路は，条件１より\( \ \fbox {　 （ウ） 　} \ \)回路である。

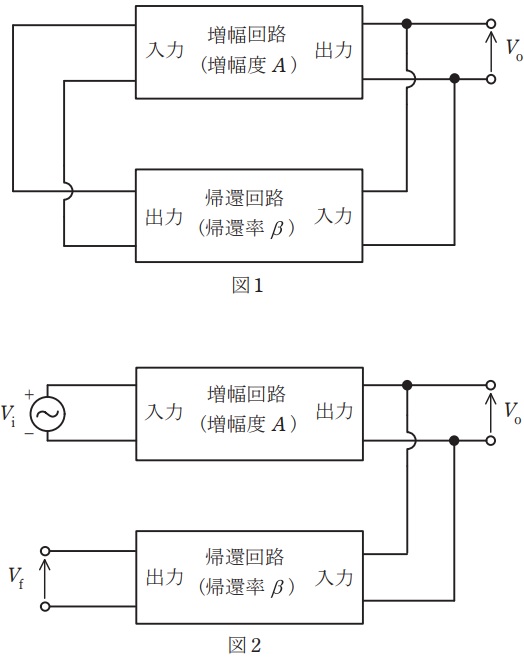
上記の記述中の空白箇所(ア)～(ウ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　同相　 & 　A\beta ≧1　 & 　正帰還　 \\
\hline
(2) & 　逆相　 & 　A\beta ≦1　 & 　負帰還　 \\
\hline
(3) & 　同相　 & 　A\beta ＜1　 & 　負帰還　 \\
\hline
(4) & 　逆相　 & 　A\beta ≧1　 & 　正帰還　 \\
\hline
(5) & 　同相　 & 　A\beta ＜1　 & 　正帰還　 \\
\hline
\end{array}
\]

【ワンポイント解説】

発振回路の発振条件に関する問題です。
正帰還増幅回路か負帰還増幅回路かはフィードバック信号をプラスとして入力するかマイナスとして入力するかによって変わります。
電子回路の専門書を見ると詳しく記載がありますが，電験対策としては概要で十分ですので，理解しておくようにして下さい。

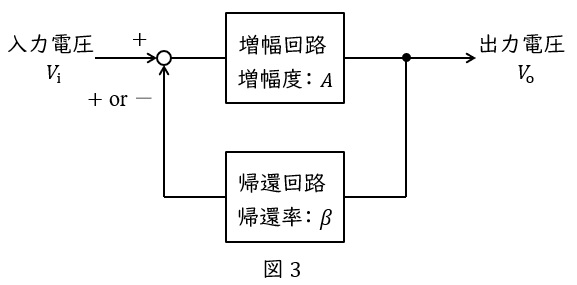
1.正帰還増幅回路と負帰還増幅回路の電圧増幅率
出力をプラスで帰還するものを正帰還増幅回路，マイナスで帰還するものを負帰還増幅回路といい，各増幅率は以下の通り求められます。正帰還増幅回路の方が電圧増幅率は大きくなりますが，負帰還増幅回路は電源電圧の変動に対して安定的になる，ひずみや外乱が抑制される，増幅回路の利得が一定となる帯域幅が大きくなる，等のメリットがあります。

①正帰還増幅回路
図3において，
\[
\begin{eqnarray}
\left( V_{\mathrm {i}}+\beta V_{\mathrm {o}}\right) A &=&V_{\mathrm {o}} \\[ 5pt ] AV_{\mathrm {i}}+A\beta V_{\mathrm {o}}&=&V_{\mathrm {o}} \\[ 5pt ] AV_{\mathrm {i}}&=&V_{\mathrm {o}}-A\beta V_{\mathrm {o}} \\[ 5pt ] AV_{\mathrm {i}}&=&\left( 1-A\beta \right) V_{\mathrm {o}} \\[ 5pt ] \frac {V_{\mathrm {o}}}{V_{\mathrm {i}}}&=&\frac {A}{1-A\beta } \\[ 5pt ] \end{eqnarray}
\]

②負帰還増幅回路
図3において，
\[
\begin{eqnarray}
\left( V_{\mathrm {i}}-\beta V_{\mathrm {o}}\right) A &=&V_{\mathrm {o}} \\[ 5pt ] AV_{\mathrm {i}}-A\beta V_{\mathrm {o}}&=&V_{\mathrm {o}} \\[ 5pt ] AV_{\mathrm {i}}&=&V_{\mathrm {o}}+A\beta V_{\mathrm {o}} \\[ 5pt ] AV_{\mathrm {i}}&=&\left( 1+A\beta \right) V_{\mathrm {o}} \\[ 5pt ] \frac {V_{\mathrm {o}}}{V_{\mathrm {i}}}&=&\frac {A}{1+A\beta } \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(1)
(ア)
発振回路を継続させるには，増幅回路の入力電圧\( \ V_{\mathrm {i}} \ \)と帰還回路の出力電圧\( \ V_{\mathrm {f}} \ \)は同相である必要があります。これを発振回路の周波数条件と言います。

(イ)
図2において，発振回路を継続させるには，\( \ V_{\mathrm {f}}≧V_{\mathrm {i}} \ \)すなわち，
\[
\begin{eqnarray}
V_{\mathrm {f}}&≧&V_{\mathrm {i}} \\[ 5pt ] A\beta V_{\mathrm {i}} &≧&V_{\mathrm {i}} \\[ 5pt ] A\beta &≧&1 \\[ 5pt ] \end{eqnarray}
\] の条件が必要となります。これを発振回路の振幅条件といいます。

(ウ)
図1の回路は出力に\( \ \beta \ \)をかけたものをそのまま同相で入力しているので，正帰還回路となります。