Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,真空中における電子の運動に関する記述である。
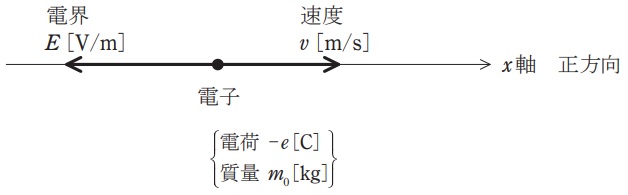
図のように,\( \ x \ \)軸上の負の向きに大きさが一定の電界\( \ E \ \mathrm {[V/m]} \ \)が存在しているとき,\( \ x \ \)軸上に電荷が\( \ -e \ \mathrm {[C]} \ \)(\( \ e \ \)は電荷の絶対値),質量\( \ m_{0} \ \mathrm {[kg]} \ \)の\( \ 1 \ \)個の電子を置いた場合を考える。\( \ x \ \)軸の正方向の電子の加速度を\( \ a \ \mathrm {[m/s^{2}]} \ \)とし,また,この電子に加わる力の正方向を\( \ x \ \)軸の正方向にとったとき,電子の運動方程式は
\[
\begin{eqnarray}
m_{0}a &=& \ \fbox { (ア) } \ ・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。①式から電子は等加速度運動をすることがわかる。したがって,電子の初速度を零としたとき,\( \ x \ \)軸の正方向に向かう電子の速度\( \ v \ \mathrm {[m/s]} \ \)は時間\( \ t \ \mathrm {[s]} \ \)の\( \ \fbox { (イ) } \ \)関数となる。また,電子の走行距離\( \ x_{\mathrm {dis}} \ \mathrm {[m]} \ \)は時間\( \ t \ \mathrm {[s]} \ \)の\( \ \fbox { (ウ) } \ \)関数で表される。さらに,電子の運動エネルギーは時間\( \ t \ \mathrm {[s]} \ \)の\( \ \fbox { (エ) } \ \)で増加することがわかる。
ただし,電子の速度\( \ v \ \mathrm {[m/s]} \ \)はその質量の変化が無視できる範囲とする。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & eE & 一 次 & 二 次 & 1 乗 \\
\hline
(2) & \displaystyle \frac {1}{2}eE & 二 次 & 一 次 & 1 乗 \\
\hline
(3) & eE^{2} & 一 次 & 二 次 & 2 乗 \\
\hline
(4) & \displaystyle \frac {1}{2}eE & 二 次 & 一 次 & 2 乗 \\
\hline
(5) & eE & 一 次 & 二 次 & 2 乗 \\
\hline
\end{array}
\]
【ワンポイント解説】
電界中の電子の運動は数年に一回程度,形を変えて出題されるイメージです。考え方は同じなので,基本公式を確実に理解しておけば良いと思います。
本問で扱う公式は電気としては電子の運動以外あまり使用しない公式ばかりですが,いずれも基本公式となるので,しっかりと理解し得点源にできるようにしておきましょう。
本問は平成23年問12からの再出題となります。
1.電荷に働く力の大きさ
一様な電界\( \ E \ \mathrm {[V/m]} \ \)が電荷\( \ q \ \mathrm {[C]} \ \)にかかっているとき,この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.運動方程式(力学)
質量\( \ m \ \mathrm {[kg]} \ \)の物体に力\( \ F \ \mathrm {[N]} \ \)がかかっている時,この物体にかかる加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)との間には,
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
3.物体の運動に関する公式(力学)
初速度が\( \ v_{0} \ \mathrm {[m/s]} \ \)の物体が加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)で運動している時,\( \ t \ \mathrm {[s]} \ \) 後の物体の速度は,
\[
\begin{eqnarray}
v&=&v_{0}+at \\[ 5pt ]
\end{eqnarray}
\]
となります。
また,基準となる位置\( \ x_{0} \ \mathrm {[m]} \ \)にある物体が,初速度\( \ v_{0} \ \mathrm {[m/s]} \ \),加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)で運動しているとすると,時刻\( \ t \ \mathrm {[s]} \ \)後の位置\( \ x \ \mathrm {[m]} \ \)は,
\[
\begin{eqnarray}
x &=&x_{0}+v_{0}t+\frac {1}{2}at^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.物体の運動エネルギー(力学)
質量\( \ m \ \mathrm {[kg]} \ \)の物体が,速度\( \ v \ \mathrm {[m/s]} \ \)で運動しているときの運動エネルギー\( \ K \ \mathrm {[J]} \ \)は,
\[
\begin{eqnarray}
K &=&\frac {1}{2}mv^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(5)
(ア)
電界\( \ E \ \mathrm {[V/m]} \ \)が負の向きであるため,電子\( \ -e \ \mathrm {[C]} \ \)に働く力\( \ F \ \mathrm {[N]} \ \)は,ワンポイント解説「1.電荷に働く力の大きさ」の通り,
\[
\begin{eqnarray}
F &=&-e\cdot \left( -E\right) \\[ 5pt ]
&=&eE \\[ 5pt ]
\end{eqnarray}
\]
となり,正の向きであることがわかる。したがって,求める運動方程式は,ワンポイント解説「2.運動方程式(力学)」より,
\[
\begin{eqnarray}
m_{0}a &=&F \\[ 5pt ]
&=&eE \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
(ア)の解答式より,電子の加速度\( \ a \ \mathrm {[m/s^{2}]} \ \)は,
\[
\begin{eqnarray}
a &=&\frac {eE}{m_{0}} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ t \ \mathrm {[s]} \ \)後の\( \ x \ \)軸の正方向に向かう電子の速度\( \ v \ \mathrm {[m/s]} \ \)は,ワンポイント解説「3.物体の運動に関する公式(力学)」の通り,
\[
\begin{eqnarray}
v&=&at \\[ 5pt ]
&=&\frac {eEt}{m_{0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,時間\( \ t \ \mathrm {[s]} \ \)の一次関数となる。
(ウ)
電子の動き出した位置を\( \ x_{0} \ \mathrm {[m]} \ \)としたときの\( \ t \ \mathrm {[s]} \ \)後の電子の走行距離\( \ x_{\mathrm {dis}} \ \mathrm {[m]} \ \)は,ワンポイント解説「3.物体の運動に関する公式(力学)」の通り,
\[
\begin{eqnarray}
x_{\mathrm {dis}} &=&x_{0}+\frac {1}{2}at^{2} \\[ 5pt ]
&=&x_{0}+\frac {eEt^{2}}{2m_{0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,時間\( \ t \ \mathrm {[s]} \ \)の二次関数となる。
(エ)
電子の運動エネルギー\( \ K \ \mathrm {[J]} \ \)は,ワンポイント解説「4.物体の運動エネルギー(力学)」の通り,
\[
\begin{eqnarray}
K &=&\frac {1}{2}m_{0}v^{2} \\[ 5pt ]
&=&\frac {1}{2}m_{0}\left( \frac {eEt}{m_{0}}\right) ^{2} \\[ 5pt ]
&=& \frac {e^{2}E^{2}t^{2}}{2m_{0}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,時間\( \ t \ \mathrm {[s]} \ \)の\( \ 2 \ \)乗で増加する。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは