Contents
【問題】
【難易度】★★★★☆(やや難しい)
図1のように,相電圧\( \ 200 \ \mathrm {V} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \)の対称三相交流電源に,抵抗とインダクタンスからなる三相平衡負荷を接続した交流回路がある。次の(a)及び(b)の問に答えよ。
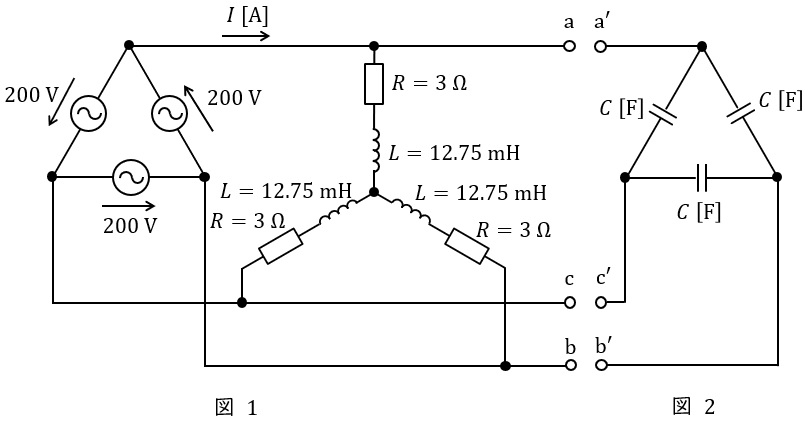
(a) 図1の回路において,負荷電流\( \ I \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 22.2 \ \) (2) \( \ 23.1 \ \) (3) \( \ 40 \ \) (4) \( \ 66.6 \ \) (5) \( \ 69.2 \ \)
(b) 図2のように,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサを\( \ \Delta \ \)結線して,その端子\( \ \mathrm {a}^{\prime } \ \),\( \ \mathrm {b}^{\prime } \ \)及び\( \ \mathrm {c}^{\prime } \ \)をそれぞれ図1の端子\( \ \mathrm {a} \ \),\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)に接続した。その結果,三相交流電源から見た負荷の力率は\( \ 1 \ \)になったという。静電容量\( \ C \ \)の値\( \ \mathrm {[F]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 1.9\times 10^{-6} \ \) (2) \( \ 1.7\times 10^{-4} \ \) (3) \( \ 2.1\times 10^{-4} \ \)
(4) \( \ 7.4\times 10^{-4} \ \) (5) \( \ 5.9\times 10^{-2} \ \)
【ワンポイント解説】
三相平衡誘導性負荷を接続した回路の電流,さらに力率調整用コンデンサを接続した回路に関する問題です。
最初は難易度が高いと感じるかもしれませんが,慣れてしまえば比較的容易に解法が見えてくる問題です。ぜひ三相交流の問題をたくさん取り組み慣れてしまうようにして下さい。
本問は平成16年問16からの再出題となります。
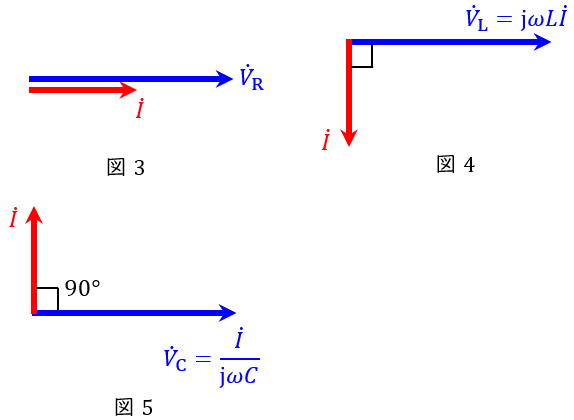
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
となります。この関係をベクトル図に表すと,図3~図5となります。
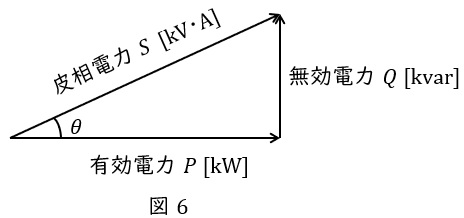
2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び,図6のようにベクトル図を描きます。さらに,有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図6において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
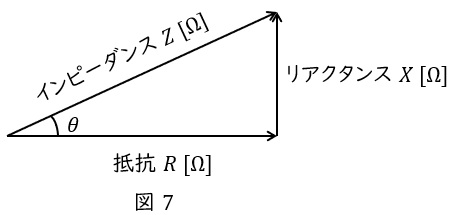
また,線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \),有効電力\( \ P \ \mathrm {[W]} \ \),無効電力\( \ Q \ \mathrm {[var]} \ \)は,インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \),抵抗を\( \ R \ \mathrm {[\Omega ]} \ \),リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ]
P &=&RI^{2} \\[ 5pt ]
Q &=&XI^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ Z \ \mathrm {[\Omega ]} \ \),\( \ R \ \mathrm {[\Omega ]} \ \),\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図7のような関係を描くことができます。
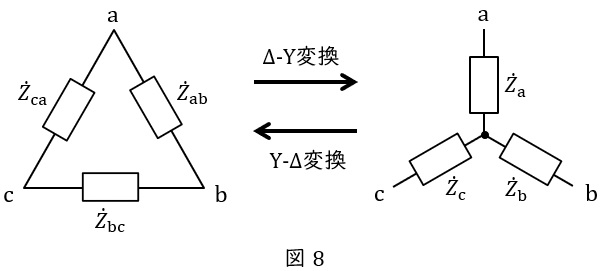
3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図8において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図8において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
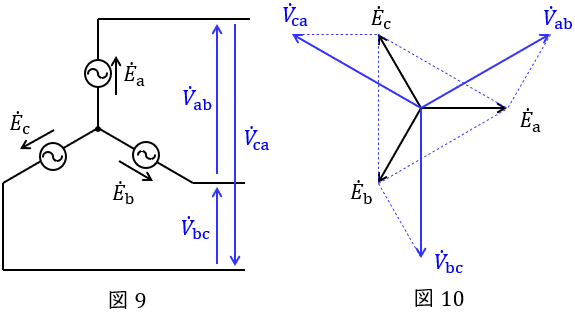
4.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図9のような三相対称電源がある時,線間電圧と相電圧の関係は図10のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。
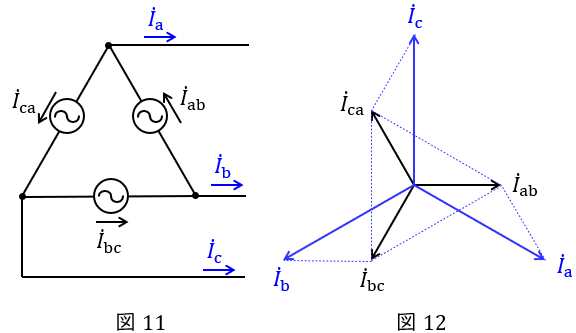
5.\( \ \Delta \ \)結線における相電流と線電流の関係
図11のような三相対称電源がある時,線電流と相電流の関係は図12のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)遅れであることが分かります。
【解答】
(a)解答:(2)
図1の回路について,ワンポイント解説「4.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り,\( \ \mathrm {Y} \ \)結線においては相電圧は線間電圧の\( \ \displaystyle \frac {1}{\sqrt {3}} \ \)倍であるから,一相分等価回路は図13のようになる。
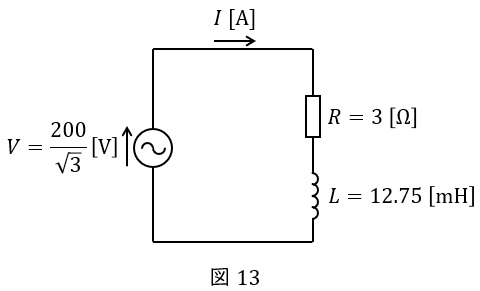
インダクタンス\( \ L=12.75 \ \mathrm {[mH]} \ \)のリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り,
\[
\begin{eqnarray}
X_{\mathrm {L}} &=&2\pi fL \\[ 5pt ]
&=&2\pi \times 50 \times 12.75 \times 10^{-3} \\[ 5pt ]
&≒&4.006 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,回路のインピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
Z &=&\sqrt {R^{2}+{X_{\mathrm {L}}}^{2}} \\[ 5pt ]
&=&\sqrt {3^{2}+4.006^{2}} \\[ 5pt ]
&≒&5.005 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,求める電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=&\frac {V}{Z} \\[ 5pt ]
&=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{5.005} \\[ 5pt ]
&≒&23.07 → 23.1 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ 試験本番では\( \ X_{\mathrm {L}}=4 \ \mathrm {[\Omega ]} \ \)で計算すれば十分かと思います。
(b)解答:(2)
静電容量\( \ C \ \mathrm {[F]} \ \)を\( \ \Delta -\mathrm {Y} \ \)変換した値\( \ C_{\mathrm {Y}} \ \mathrm {[F]} \ \)は,ワンポイント解説「3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,
\[
\begin{eqnarray}
\frac {1}{2\pi fC_{\mathrm {Y}}}&=&\frac {1}{3}\frac {1}{2\pi fC} \\[ 5pt ]
\frac {1}{C_{\mathrm {Y}}}&=&\frac {1}{3C} \\[ 5pt ]
C_{\mathrm {Y}}&=&3C \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,一相分等価回路は図14のようになる。
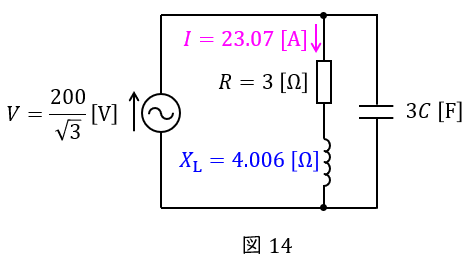
図14において,力率が\( \ 1 \ \)なので,回路で消費される遅れ無効電力と進み無効電力が等しくないといけないから,
\[
\begin{eqnarray}
X_{\mathrm {L}}I^{2}&=&\frac {V^{2}}{\displaystyle \frac {1}{2\pi f \cdot 3C}} \\[ 5pt ]
&=&6\pi fCV^{2} \\[ 5pt ]
\end{eqnarray}
\]
となる必要がある。これより\( \ C \ \mathrm {[F]} \ \)は,
\[
\begin{eqnarray}
C&=&\frac {X_{\mathrm {L}}I^{2}}{6\pi fV^{2}} \\[ 5pt ]
&=&\frac {4.006\times 23.07^{2}}{6\pi \times 50\times \left( \displaystyle \frac {200}{\sqrt {3}}\right) ^{2}} \\[ 5pt ]
&≒&0.000 \ 170 → 1.7\times 10^{-4} \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは