Contents
【問題】
【難易度】★★★★☆(やや難しい)
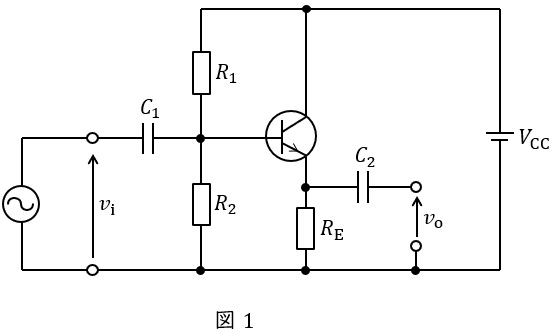
エミッタホロワ回路について,次の(a)及び(b)の問に答えよ。
(a) 図1の回路で\( \ V_{\mathrm {CC}}=9 \ \mathrm {V} \ \),\( \ R_{1}=3 \ \mathrm {k\Omega } \ \),\( \ R_{2}=6 \ \mathrm {k\Omega } \ \)とする。動作点におけるエミッタ電流を\( \ 2 \ \mathrm {mA} \ \)としたい。抵抗\( \ R_{\mathrm {E}} \ \)の値\( \ \mathrm {[k\Omega ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,動作点において,ベース電流は\( \ R_{2} \ \)を流れる直流電流より十分小さく無視できるものとし,ベース-エミッタ間電圧は\( \ 0.7 \ \mathrm {V} \ \)とする。
(1) \( \ 0.36 \ \) (2) \( \ 1.5 \ \) (3) \( \ 2.7 \ \) (4) \( \ 4.7 \ \) (5) \( \ 7.5 \ \)
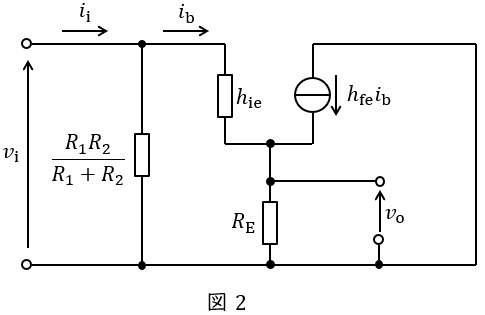
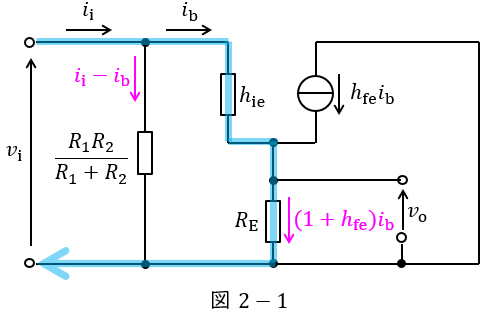
(b) 図2は,エミッタホロワ回路の交流等価回路である。ただし,使用する周波数において図1の二つのコンデンサのインピーダンスが十分に小さい場合を考えている。ここで,\( \ h_{\mathrm {ie}}=2.5 \ \mathrm {k\Omega } \ \),\( \ h_{\mathrm {fe}}=300 \ \)であり,\( \ R_{\mathrm {E}} \ \)は小問(a)で求めた値とする。入力インピーダンス\( \ \displaystyle \frac {v_{\mathrm {i}}}{i_{\mathrm {i}}} \ \)の値\( \ \mathrm {[k\Omega ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,\( \ v_{\mathrm {i}} \ \)と\( \ i_{\mathrm {i}} \ \)はそれぞれ図2に示す入力電圧と入力電流である。
(1) \( \ 2.0 \ \) (2) \( \ 15 \ \) (3) \( \ 80 \ \) (4) \( \ 300 \ \) (5) \( \ 750 \ \)
【ワンポイント解説】
エミッタホロワ回路における回路演算に関する問題です。
パターンが比較的決まっているので,何問か過去問に取り組めば解けるようになると思います。なお,(b)はいろいろな解き方がありますが,計算量は変わらないので,ここではオーソドックスなキルヒホッフの法則を使用した解答を模範解答にしています。
本問は平成30年問16の数値を少し変更した問題です。
【解答】
(a)解答:(3)
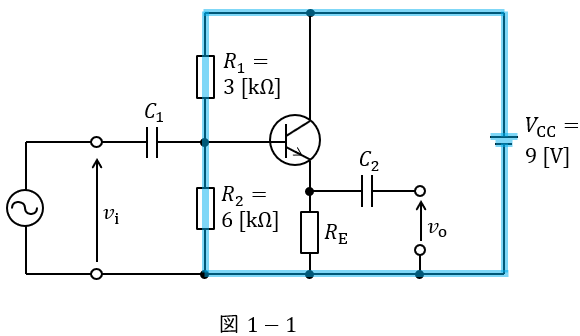
ベース電流は十分に小さく無視できるので,図1-1に示す閉回路に分圧の法則を適用すると,トランジスタのベース電圧\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {B}} &=&\frac {R_{2}}{R_{1}+R_{2}}V_{\mathrm {CC}} \\[ 5pt ]
&=&\frac {6\times 10^{3}}{3\times 10^{3}+6\times 10^{3}}\times 9 \\[ 5pt ]
&=&6 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
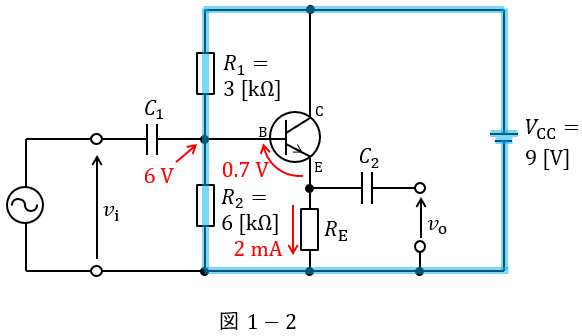
題意より,ベース-エミッタ間電圧\( \ V_{\mathrm {BE}}=0.7 \ \mathrm {[V]} \ \)であるから,エミッタ電圧\( \ V_{\mathrm {E}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {E}} &=&V_{\mathrm {B}}-0.7 \\[ 5pt ]
&=&6-0.7 \\[ 5pt ]
&=&5.3 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,エミッタ電流\( \ i_{\mathrm {E}}=2 \ \mathrm {[mA]} \ \)であるから,\( \ R_{\mathrm {E}} \ \mathrm {[k\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {E}} &=&\frac {V_{\mathrm {E}}}{i_{\mathrm {E}}} \\[ 5pt ]
&=&\frac {5.3}{2\times 10^{-3}} \\[ 5pt ]
&=&2.65\times 10^{3} \ \mathrm {[\Omega ]} → 2.7 \ \mathrm {[k\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
図2-1に示す回路において,\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)と青矢印で示した回路の電圧降下及び\( \ \displaystyle \frac {R_{1}R_{2}}{R_{1}+R_{2}} \ \)の電圧降下は等しい。
青矢印で示した回路の電圧降下の大きさより,
\[
\begin{eqnarray}
v_{\mathrm {i}}&=&h_{\mathrm {ie}}i_{\mathrm {b}}+R_{\mathrm {E}}\left( 1+h_{\mathrm {fe}}\right) i_{\mathrm {b}} \\[ 5pt ]
&=& 2.5\times 10^{3}i_{\mathrm {b}} +2.65\times 10^{3}\times \left( 1+300 \right) i_{\mathrm {b}} \\[ 5pt ]
&=&800 \ 150 i_{\mathrm {b}} \ \mathrm {[V ]} \\[ 5pt ]
\end{eqnarray}
\]
であり,これが\( \ \displaystyle \frac {R_{1}R_{2}}{R_{1}+R_{2}} \ \)での電圧降下と等しいことから,
\[
\begin{eqnarray}
\frac {R_{1}R_{2}}{R_{1}+R_{2}}\left( i_{\mathrm {i}}-i_{\mathrm {b}}\right) &=&800 \ 150 i_{\mathrm {b}} \\[ 5pt ]
\frac {3\times 10^{3} \times 6\times 10^{3}}{3\times 10^{3} + 6\times 10^{3}}\left( i_{\mathrm {i}}-i_{\mathrm {b}}\right) &=&800 \ 150 i_{\mathrm {b}} \\[ 5pt ]
2 \ 000\left( i_{\mathrm {i}}-i_{\mathrm {b}}\right) &=&800 \ 150 i_{\mathrm {b}} \\[ 5pt ]
2 \ 000 i_{\mathrm {i}}-2 \ 000i_{\mathrm {b}} &=&800 \ 150 i_{\mathrm {b}} \\[ 5pt ]
2 \ 000i_{\mathrm {i}}&=&802 \ 150 i_{\mathrm {b}} \\[ 5pt ]
i_{\mathrm {i}}&≒&401 i_{\mathrm {b}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,入力インピーダンス\( \ \displaystyle \frac {v_{\mathrm {i}}}{i_{\mathrm {i}}} \ \mathrm {[k\Omega ]} \ \)は,
\[
\begin{eqnarray}
\frac {v_{\mathrm {i}}}{i_{\mathrm {i}}} &=&\frac {800 \ 150 i_{\mathrm {b}}}{401 i_{\mathrm {b}}} \\[ 5pt ]
&≒&1 \ 995 \ \mathrm {[\Omega ]} → 2.0 \ \mathrm {[k\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは