《理論》〈電磁気〉[H29:問3]合成インダクタンスに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

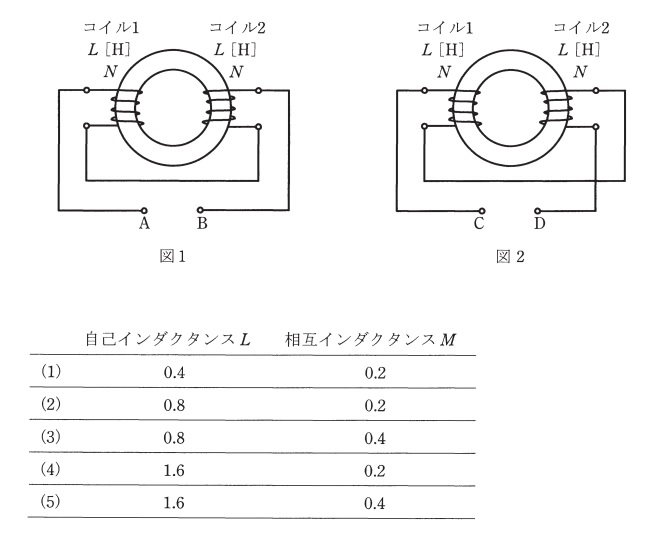
環状鉄心に，コイル1及びコイル2が巻かれている。二つのコイルを図1のように接続したとき，端子\( \ \mathrm{A}-\mathrm{B} \ \)間の合成インダクタンスの値は\( \ 1.2 \ \mathrm{H} \ \)であった。次に，図2のように接続したとき，端子\( \ \mathrm{C}-\mathrm{D} \ \)間の合成インダクタンスの値は\( \ 2.0 \ \mathrm{H} \ \)であった。このことから，コイル1の自己インダクタンス\( \ L \ \)の値\( \ \left[ \mathrm{H}\right] \ \)，コイル1及びコイル2の相互インダクタンス\( \ M \ \)の値\( \ \left[ \mathrm{H}\right] \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
ただし，コイル1及びコイル2の自己インダクタンスはともに\( \ L \ \left[ \mathrm{H}\right] \ \)，その巻数を\( \ N \ \)とし，また，鉄心は等断面，等質であるとする。

【ワンポイント解説】

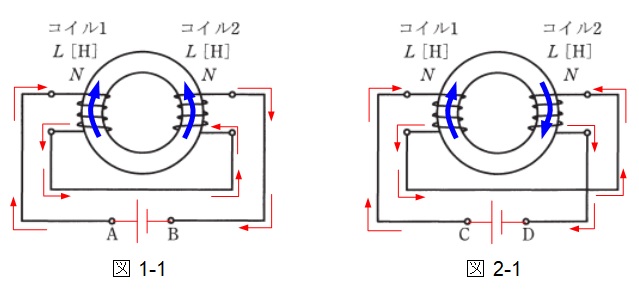
図1と図2に同電圧の電源を接続したときの電流の向きと発生する磁束の向きは図1-1，図2-1の通りとなります。図1-1は磁束を弱め合う接続なので差動接続，図2-1は磁束を強め合う接続なので和動接続と言います。

1.合成インダクタンス\( \ L_{0} \ \)
自己インダクタンスが\( \ L_{1} \ \left[ \mathrm{H}\right] \ \)と\( \ L_{2} \ \left[ \mathrm{H}\right] \ \)を接続した時の合成インダクタンス\( \ L_{0} \ \)は，相互インダクタンスを\( \ M \ \left[ \mathrm{H}\right] \ \)が与えられている時，以下の式で求められます。

①差動接続時(図1-1)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}-2M \\[ 5pt ] \end{eqnarray}
\] ②和動接続時(図2-1)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}+2M \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(2)
題意より，図1の差動接続時の合成インダクタンスが\( \ 1.2 \ \mathrm{H} \ \)であるから，
\[
\begin{eqnarray}
L+L-2M&=&1.2 \\[ 5pt ] 2L-2M&=&1.2 \\[ 5pt ] L-M&=&0.6　・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。また，図2の和動接続時の合成インダクタンスが\( \ 2.0 \ \mathrm{H} \ \)であるから，
\[
\begin{eqnarray}
L+L+2M&=&2.0 \\[ 5pt ] 2L+2M&=&2.0 \\[ 5pt ] L+M&=&1.0　・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] となる。①＋②より，
\[
\begin{eqnarray}
2L&=&1.6 \\[ 5pt ] L&=&0.8 \\[ 5pt ] \end{eqnarray}
\] ②－①より，
\[
\begin{eqnarray}
2M&=&0.4 \\[ 5pt ] M&=&0.2 \\[ 5pt ] \end{eqnarray}
\] と求められる。