《電力》〈変電〉[R3:問9]変圧器故障時の過負荷運転に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

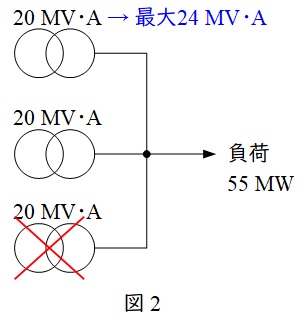
$\ 1 \ $台の定格容量が$\ 20 \ \mathrm {MV\cdot A} \ $の三相変圧器を$\ 3 \ $台有する配電用変電所があり，その総負荷が$\ 55 \ \mathrm {MW} \ $である。変圧器$\ 1 \ $台が故障したときに，残りの変圧器の過負荷運転を行い，不足分を他の変電所に切り換えることにより，故障発生前と同じ電力を供給したい。この場合，他の変電所に故障発生前の負荷の何$\ \mathrm {％} \ $を直ちに切り換える必要があるか，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，残りの健全な変圧器は，変圧器故障時に定格容量の$\ 120 \ \mathrm {％} \ $の過負荷運転をすることとし，力率は常に$\ 95 \ \mathrm {％} \ $（遅れ）で変化しないものとする。

　(1)　$\ 6.2 \ $　　(2)　$\ 10.0 \ $　　(3)　$\ 12.1 \ $　　(4)　$\ 17.1 \ $　　(5)　$\ 24.2 \ $

【ワンポイント解説】

変圧器の容量及び力率計算に関する問題です。
平成26年問6に類題も出題されていますので，過去問をしっかりと取り組んだ方は得点できたのではないかと思います。

1.力率$\ \cos \theta \ $
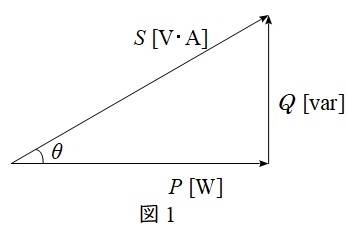
電圧と電流の位相差が$\ \theta \ $(電流が遅れ)である時，皮相電力$\ S \ \mathrm {[kV\cdot A]} \ $，有効電力$\ P \ \mathrm {[kW]} \ $，無効電力$\ Q \ \mathrm {[kvar]} \ $の関係は図1のように描くことができ，

$$\begin{eqnarray} \cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}$$ を力率と言います。

【解答】

解答：(4)
健全な変圧器は，定格容量$\ S_{\mathrm {n}}=20 \ \mathrm {[MV\cdot A]} \ $の$\ 120 \ \mathrm {％} \ $で過負荷運転できるので，その容量$\ S_{\mathrm {o}} \ \mathrm {[MV\cdot A]} \ $は，

$$\begin{eqnarray} S_{\mathrm {o}} &=&S_{\mathrm {n}}\times 1.2 \\[ 5pt ] &=&20\times 1.2 \\[ 5pt ] &=&24 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}$$ となる。力率が$\ 95 \ \mathrm {％} \ $（遅れ）であるので，負荷の皮相電力$\ S_{\mathrm {L}} \ \mathrm {[MV\cdot A]} \ $は，ワンポイント解説「1.力率$\ \cos \theta \ $」の通り，
$$\begin{eqnarray} S_{\mathrm {L}} &=&\frac {P_{\mathrm {L}}}{\cos \theta } \\[ 5pt ] &=&\frac {55}{0.95} \\[ 5pt ] &≒&57.89 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}$$ となる。したがって，過負荷容量$\ \Delta S \ \mathrm {[MV\cdot A]} \ $は，
$$\begin{eqnarray} \Delta S &=&S_{\mathrm {L}}-2S_{\mathrm {o}} \\[ 5pt ] &=&57.89-2\times 24 \\[ 5pt ] &=&9.89 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}$$ となるので，切り換える負荷の割合は，
$$\begin{eqnarray} \frac {\Delta S}{S_{\mathrm {L}}}\times 100 &=&\frac {9.89}{57.89}\times 100 \\[ 5pt ] &≒&17.1 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}$$ と求められる。