Contents
【問題】
【難易度】★★★☆☆(普通)
図のような環状鉄心に巻かれたコイルがある。
図の環状コイルについて,
・端子\( \ 1-2 \ \)間の自己インダクタンスを測定したところ,\( \ 40 \ \mathrm {mH} \ \)であった。
・端子\( \ 3-4 \ \)間の自己インダクタンスを測定したところ,\( \ 10 \ \mathrm {mH} \ \)であった。
・端子\( \ 2 \ \)と\( \ 3 \ \)を接続した状態で端子\( \ 1-4 \ \)間のインダクタンスを測定したところ,\( \ 86 \ \mathrm {mH} \ \)であった。
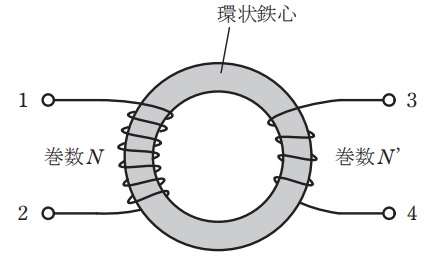
このとき,端子\( \ 1-2 \ \)間のコイルと端子\( \ 3-4 \ \)間のコイルとの間の結合係数\( \ k \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.81 \ \) (2) \( \ 0.90 \ \) (3) \( \ 0.95 \ \) (4) \( \ 0.98 \ \) (5) \( \ 1.8 \ \)
【ワンポイント解説】
自己インダクタンスと合成インダクタンスから結合係数を求める問題です。
結合係数の公式と合成インダクタンスの両方の公式を覚えている上で計算する必要があります。
結合係数は\( \ 1 \ \)以下であることを知っていれば(5)の選択肢は除外できるので,覚えておくようにしましょう。
1.自己インダクタンスの定義\( \ L \ \)
コイルの巻き数が\( \ N \ \)として,電流\( \ I \ \)を流した時の鎖交磁束が\( \ \phi \ \)だった時,自己インダクタンス\( \ L \ \)と鎖交磁束\( \ \phi \ \)の関係は,
\[
\begin{eqnarray}
LI&=&N\phi \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.相互インダクタンス\( \ M \ \)
自己インダクタンス\( \ L_{1} \ \)と\( \ L_{2} \ \)のコイルがあった時の相互インダクタンス\( \ M \ \)は,
\[
\begin{eqnarray}
M&=&k\sqrt {L_{1}L_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。この時,\( \ k \ \)は結合係数と呼ばれ,\( \ 0≦k≦1 \ \)となります。
3.合成インダクタンス\( \ L_{0} \ \)
自己インダクタンス\( \ L_{1} \ \left[ \mathrm{H}\right] \ \)と\( \ L_{2} \ \left[ \mathrm{H}\right] \ \)のコイルを接続した時の合成インダクタンス\( \ L_{0} \ \left[ \mathrm{H}\right] \ \)は,相互インダクタンス\( \ M \ \left[ \mathrm{H}\right] \ \)が与えられている時,以下の式で求められます。
①和動接続(磁束が強め合う)時(図1)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}+2M \\[ 5pt ]
\end{eqnarray}
\]
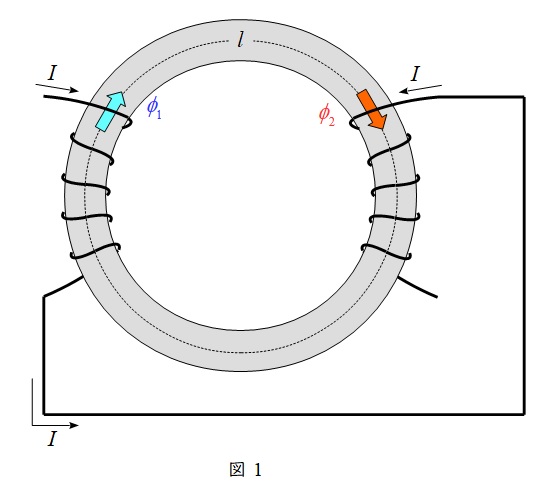
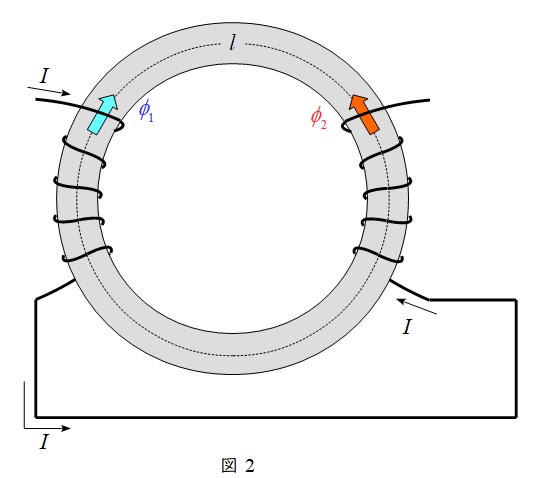
②差動接続(磁束が弱め合う)時(図2)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}-2M \\[ 5pt ]
\end{eqnarray}
\]
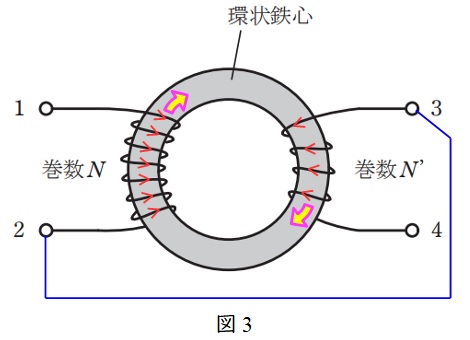
【解答】
解答:(2)
端子\( \ 1-2 \ \)間の自己インダクタンスを\( \ L_{12}=40 \ \mathrm {[mH]} \ \),端子\( \ 3-4 \ \)間の自己インダクタンスを\( \ L_{34}=10 \ \mathrm {[mH]} \ \)とおくと,相互インダクタンス\( \ M \ \)は,結合係数を\( \ k \ \)とすると,ワンポイント解説「2.相互インダクタンス\( \ M \ \)」の通り,
\[
\begin{eqnarray}
M&=&k\sqrt {L_{12}L_{34}} \\[ 5pt ]
&=&k\sqrt {40\times 10} \\[ 5pt ]
&=&20k \ \mathrm {[mH]} \\[ 5pt ]
\end{eqnarray}
\]
となる。図3に示すように,端子\( \ 2 \ \)と\( \ 3 \ \)を接続した状態は和動接続となるため,合成インダクタンス\( \ L_{0} \ \)は,ワンポイント解説「3.合成インダクタンス\( \ L_{0} \ \)」の通り,
\[
\begin{eqnarray}
L_{0}&=&L_{12}+L_{34}+2M \\[ 5pt ]
\end{eqnarray}
\]
となるため,各値を代入すれば,
\[
\begin{eqnarray}
86&=&40+10+2\cdot 20k \\[ 5pt ]
40k&=&36 \\[ 5pt ]
k&=&0.90 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは