《理論》〈電気回路〉[H22:問9]三相平衡回路における電圧，電流及び電力の関係に関する論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

\( \ \mathrm {Y} \ \)結線の対称三相交流電源に\( \ \mathrm {Y} \ \)結線の平衡三相抵抗負荷を接続した場合を考える。負荷側における線間電圧を\( \ V_{\mathrm {ℓ}} \ \mathrm {[V]} \ \)，線電流を\( \ I_{\mathrm {ℓ}} \ \mathrm {[A]} \ \)，相電圧を\( \ V_{\mathrm {p}} \ \mathrm {[V]} \ \)，相電流を\( \ I_{\mathrm {p}} \ \mathrm {[A]} \ \)，各相の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)，三相負荷の消費電力を\( \ P \ \mathrm {[W]} \ \)とする。このとき，誤っているのは次のうちどれか。

(1)　\( \ V_{\mathrm {ℓ}} = \sqrt {3}V_{\mathrm {p}} \ \)が成り立つ。

(2)　\( \ I_{\mathrm {ℓ}} = I_{\mathrm {p}} \ \)が成り立つ。

(3)　\( \ \displaystyle I_{\mathrm {ℓ}} = \frac {V_{\mathrm {p}}}{R} \ \)が成り立つ。

(4)　\( \ P = \sqrt {3}V_{\mathrm {p}}I_{\mathrm {p}} \ \)が成り立つ。

(5)　電源と負荷の中性点を中性線で接続しても，中性線に電流は流れない。

【ワンポイント解説】

対称三相回路の電圧，電流及び電力の関係に関する問題です。
ワンポイント解説では電源側で描いていますが，負荷側でも同様な関係が成立します。
このような問題は図1，図2のような回路図やベクトル図を描くとイメージがしやすくなるかと思いますので，試験本番でも手早く描くと良いでしょう。

1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
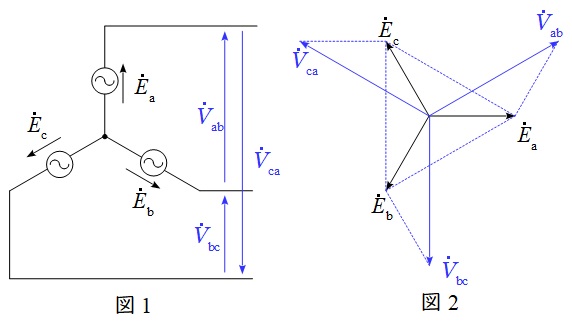
図1のような三相対称電源がある時，線間電圧と相電圧の関係は図2のベクトル図のようになり，線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ] V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ] V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)進みであることが分かります。

2.\( \ \Delta \ \)結線における相電流と線電流の関係
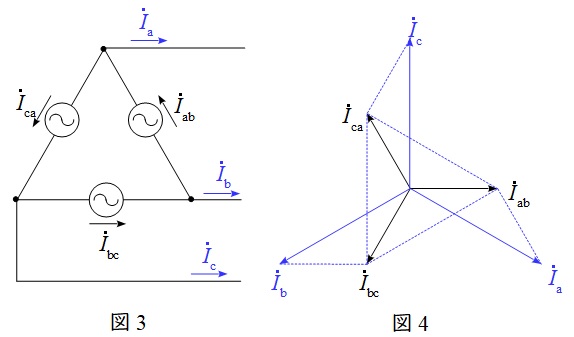
図3のような三相対称電源がある時，線電流と相電流の関係は図4のベクトル図のようになり，線電流の大きさは相電流の大きさと比較すると，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ] I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ] I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)遅れであることが分かります。

【解答】

解答：(4)
(1)正しい
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，線間電圧は相電圧の\( \ \sqrt {3} \ \)倍となるので，\( \ V_{\mathrm {ℓ}} = \sqrt {3}V_{\mathrm {p}} \ \)が成り立ちます。

(2)正しい
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」図1に示す通り，\( \ \mathrm {Y} \ \)結線においては線電流と相電流の大きさは等しく，\( \ I_{\mathrm {ℓ}} = I_{\mathrm {p}} \ \)が成り立ちます。

(3)正しい
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」図1に示す通り，抵抗\( \ R \ \)が接続されている場合には，\( \ \displaystyle I_{\mathrm {ℓ}} = \frac {V_{\mathrm {p}}}{R} \ \)が成り立ちます。

(4)誤り
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」図1に示す通り，一相あたりの消費電力が\( \ V_{\mathrm {p}}I_{\mathrm {p}} \ \)なので，三相分の消費電力は\( \ P = 3V_{\mathrm {p}}I_{\mathrm {p}} \ \)となります。線間電圧，線電流で表す場合には\( \ V_{\mathrm {ℓ}} = \sqrt {3}V_{\mathrm {p}} \ \)及び\( \ I_{\mathrm {ℓ}} = I_{\mathrm {p}} \ \)の関係から\( \ P = \sqrt {3}V_{\mathrm {ℓ}}I_{\mathrm {ℓ}} \ \)が成り立ちます。

(5)正しい
三相平衡負荷においては電源側，負荷側とも中性点の電位は零であるため，電源と負荷の中性点を中性線で接続しても，中性線に電流は流れません。