《理論》〈電気回路〉[R05下:問17]直並列されたコンデンサの合成静電容量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図1の端子$\ \mathrm {a – d} \ $間の合成静電容量について，次の(a)及び(b)の問に答えよ。

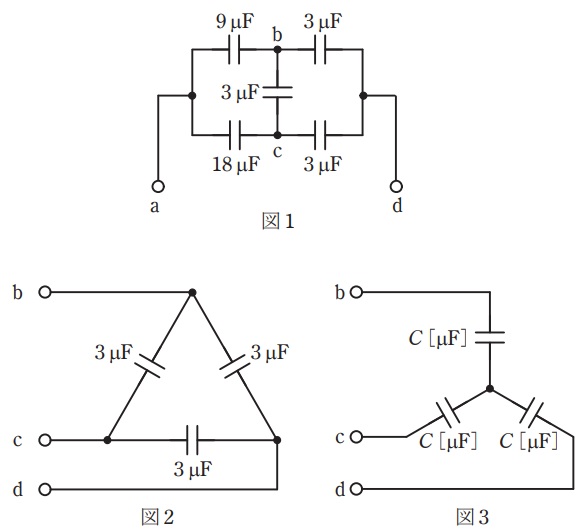
(a)　端子$\ \mathrm {b – c – d} \ $間は図2のように$\ \Delta \ $結線で接続されている。これを図3のように$\ \mathrm {Y} \ $結線に変換したとき，電気的に等価となるコンデンサ$\ C \ $の値$\ \mathrm {[\mu F]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$\ 1.0 \ $　　(2)　$\ 2.0 \ $　　(3)　$\ 4.5 \ $　　(4)　　$\ 6.0 \ $　　(5)　$\ 9.0 \ $

(b)　図3を用いて，図1の端子$\ \mathrm {b – c – d} \ $間を$\ \mathrm {Y} \ $結線回路に変換したとき，図1の端子$\ \mathrm {a – d} \ $間の合成静電容量$\ C_{0} \ $の値$\ \mathrm {[\mu F]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$\ 3.0 \ $　　(2)　$\ 4.5 \ $　　(3)　$\ 4.8 \ $　　(4)　　$\ 6.0 \ $　　(5)　$\ 9.0 \ $

【ワンポイント解説】

直並列接続したコンデンサの合成静電容量を求める問題です。
(a)は確実に得点しておきたい設問，(b)は計算間違いのないように注意しながら解いていく設問です。$\ \Delta -\mathrm {Y} \ $変換，静電容量と抵抗の考え方の違い等重要な内容を多く含みますので，ぜひ理解するようにして下さい。
本問は平成27年問16からの再出題となります。

1.抵抗，コイル，コンデンサの電圧$\ V \ \mathrm {[V]} \ $と電流$\ I \ \mathrm {[A]} \ $の関係
抵抗$\ R \ \mathrm {[\Omega ]} \ $，コイル$\ L \ \mathrm {[H]} \ $，コンデンサ$\ C \ \mathrm {[F]} \ $があり，電源の角周波数$\ \omega \ \mathrm {[rad / s]} \ $及び周波数$\ f \ \mathrm {[Hz]} \ $が与えられているとき，それぞれのインピーダンスは，
$$\begin{eqnarray} {\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}$$ で求められ，それぞれの電圧と電流の関係は，
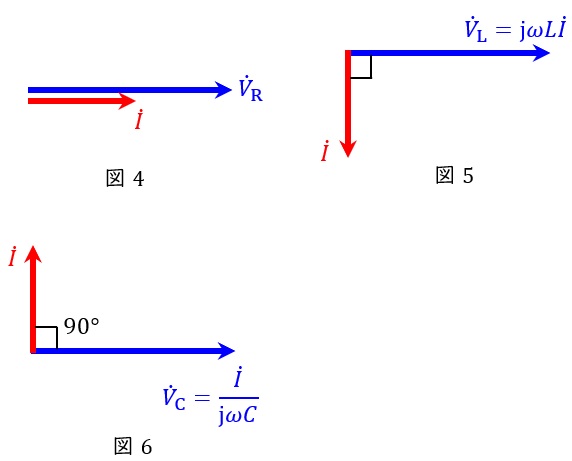
$$\begin{eqnarray} {\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}$$ となります。この関係をベクトル図に表すと，図4～図6となります。

2.コンデンサの合成静電容量
静電容量$\ C_{1} \ \mathrm {[F]} \ $と$\ C_{2} \ \mathrm {[F]} \ $の合成静電容量$\ C \ \mathrm {[F]} \ $は，
　　並列接続時：$\ C=C_{1}+C_{2} \ $
　　直列接続時：$\ \displaystyle C=\frac {1}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}}=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \ $
となります。

3.$\ \Delta -\mathrm {Y} \ $変換と$\ \mathrm {Y}-\Delta \ $変換
①$\ \Delta -\mathrm {Y} \ $変換
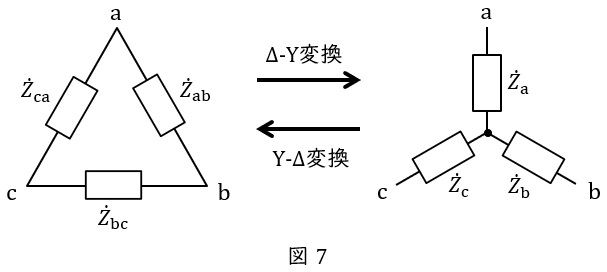
図7において，
$$\begin{eqnarray} {\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}$$ ②$\ \mathrm {Y}-\Delta \ $変換
図7において，
$$\begin{eqnarray} {\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}$$ 平衡三相回路においては，
$$\begin{eqnarray} {\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}$$ となります。

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

(a)解答：(5)
ワンポイント解説「3.$\ \Delta -\mathrm {Y} \ $変換と$\ \mathrm {Y}-\Delta \ $変換」の通り，三相平衡回路での$\ \mathrm {Y} \ $接続時のインピーダンスは$\ \Delta \ $接続時の$\ \displaystyle \frac {1}{3} \ $倍となるから，
$$\begin{eqnarray} \frac {1}{\mathrm {j}\omega C_{\mathrm {Y}}}&=&\frac {1}{3}\cdot \frac {1}{\mathrm {j}\omega C_{\mathrm {\Delta }}} \\[ 5pt ] \frac {1}{C_{\mathrm {Y}}}&=&\frac {1}{3C_{\mathrm {\Delta }}} \\[ 5pt ] C_{\mathrm {Y}}&=&3C_{\mathrm {\Delta }} \\[ 5pt ] \end{eqnarray}$$ の関係があるので，図2における$\ C \ \mathrm {[\mu F]} \ $は，
$$\begin{eqnarray} C&=&3\times 3 \\[ 5pt ] &=&9 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(b)解答：(3)
(a)の解答を元に図1の回路を整理すると図8のようになる。
$\ C_{1}=9 \ \mathrm {[\mu F]} \ $と$\ C_{3}=9 \ \mathrm {[\mu F]} \ $の合成静電容量$\ C_{13} \ \mathrm {[\mu F]} \ $は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
$$\begin{eqnarray} C_{13}&=&\frac {C_{1}C_{3}}{C_{1}+C_{3}} \\[ 5pt ] &=&\frac {9\times 9}{9+9} \\[ 5pt ] &=&4.5 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}$$ となり，$\ C_{2}=18 \ \mathrm {[\mu F]} \ $と$\ C_{4}=9 \ \mathrm {[\mu F]} \ $の合成静電容量$\ C_{24} \ \mathrm {[\mu F]} \ $は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
$$\begin{eqnarray} C_{24}&=&\frac {C_{2}C_{4}}{C_{2}+C_{4}} \\[ 5pt ] &=&\frac {18\times 9}{18+9} \\[ 5pt ] &=&6 \ \mathrm {[\mu F]} \end{eqnarray}$$ となる。よって，$\ C_{1} \ ～C_{4} \ $までの合成静電容量$\ C_{1234} \ \mathrm {[\mu F]} \ $は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
$$\begin{eqnarray} C_{1234}&=&C_{13}+C_{24} \\[ 5pt ] &=&4.5+6 \\[ 5pt ] &=&10.5 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}$$ となる。したがって，端子$\ \mathrm {a-d} \ $間の合成静電容量$\ C_{0} \ \mathrm {[\mu F]} \ $は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
$$\begin{eqnarray} C_{0}&=&\frac {C_{1234}C_{5}}{C_{1234}+C_{5}} \\[ 5pt ] &=&\frac {10.5\times 9}{10.5+9} \\[ 5pt ] &≒&4.846　→　4.8 \ \mathrm {[\mu F]} \end{eqnarray}$$ と求められる。