Contents
【問題】
【難易度】★★★☆☆(普通)
起電力が\( \ E \ \mathrm {[V]} \ \)で内部抵抗が\( \ r \ \mathrm {[\Omega ]} \ \)の電池がある。この電池に抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と可変抵抗\( \ R_{2} \ \mathrm {[\Omega ]} \ \)を並列につないだとき,抵抗\( \ R_{2} \ \mathrm {[\Omega ]} \ \)から発生するジュール熱が最大となるときの抵抗\( \ R_{2} \ \)の値\( \ \mathrm {[\Omega ]} \ \)を表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ R_{2}=r \ \) (2) \( \ R_{2}=R_{1} \ \) (3) \( \ \displaystyle R_{2}=\frac {rR_{1}}{r+R_{1}} \ \)
(4) \( \ \displaystyle R_{2}=\frac {rR_{1}}{R_{1}-r} \ \) (5) \( \ \displaystyle R_{2}=\frac {rR_{1}}{r-R_{1}} \ \)
【ワンポイント解説】
抵抗から発生するジュール熱が最大となる条件を求める問題です。
以下の解説のように,微分積分や相加相乗平均の関係を用いれば最大となる条件は求められますが,基本的には覚えておく内容と考えた方が良いでしょう。
本問は平成19年問5からの再出題となります。
1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.消費電力が最大となる条件
結論としては,ある抵抗を切り離した際にその抵抗と電源側をみた合成抵抗(ただし,電圧源は短絡)が等しい場合に消費電力が最大となります。
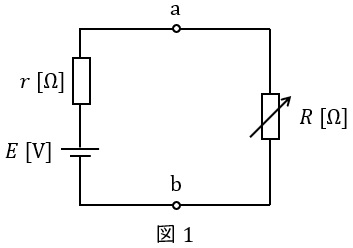
具体的に,図1に示す回路を例に説明します。
回路の合成抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{0} &=&R+r \\[ 5pt ]
\end{eqnarray}
\]
であり,回路を流れる電流\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=&\frac {E}{R_{0}} \\[ 5pt ]
&=&\frac {E}{R+r} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって,抵抗\( \ R \ \mathrm {[\Omega ]} \ \)での消費電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ]
&=&R\left( \frac {E}{R+r}\right) ^{2} \\[ 5pt ]
&=&\frac {RE}{R^{2}+2Rr+r^{2}} \\[ 5pt ]
&=&\frac {E}{\displaystyle R+2r+\frac {r^{2}}{R}} \\[ 5pt ]
\end{eqnarray}
\]
となります。上式の分母を\( \ \displaystyle A=\displaystyle R+2r+\frac {r^{2}}{R} \ \)とおくと,\( \ A \ \)が最小のとき,すなわち\( \ A \ \)を両辺\( \ R \ \)で微分したものが零となるとき消費電力\( \ P \ \mathrm {[W]} \ \)は最大となります。したがって\( \ A \ \)を両辺\( \ R \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}R} =1-\frac {r^{2}}{R^{2}}&=&0 \\[ 5pt ]
\frac {r^{2}}{R^{2}}&=&1 \\[ 5pt ]
R&=&r \\[ 5pt ]
\end{eqnarray}
\]
のとき消費電力\( \ P \ \mathrm {[W]} \ \)は最大となります。
以上からこの例においても,抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を切り離したとき,切り離した場所から電源側をみた抵抗\( \ r \ \mathrm {[\Omega ]} \ \)と等しいとき,\( \ R \ \mathrm {[\Omega ]} \ \)での消費電力は最大となります。
【解答】
解答:(3)
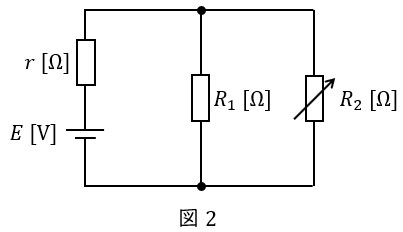
題意に沿って回路図を描くと図2のようになる。
ワンポイント解説「2.消費電力が最大となる条件」の通り,消費電力が最大となるのは,\( \ R_{2} \ \mathrm {[\Omega ]} \ \)を切り離した際の電源側をみた合成抵抗と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が等しいときであるから,
\[
\begin{eqnarray}
R_{2}&=&\frac {rR_{1}}{r+R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは