《理論》〈電磁気〉[H27:問3]強磁性体の初期磁化特性に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，ある強磁性体の初期磁化特性について述べたものである。

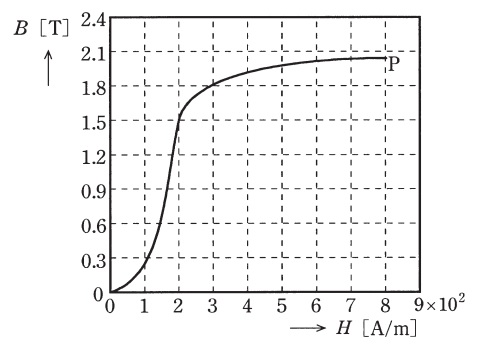
磁界の向きに強く磁化され，比透磁率\(\mu _{r}\)が\(1\)よりも非常に\(\fbox {　 （ア） 　}\)物質を強磁性体という。まだ磁化されていない強磁性体に磁界\(H \ \mathrm {[A/m]}\)を加えて磁化していくと，磁束密度\(B \ \mathrm {[T]}\)は図のように変化する。よって，透磁率\(\displaystyle \mu \ \mathrm {[H/m]}\left( =\frac {B}{H}\right) \)も磁界の強さによって変化する。図から，この強磁性体の透磁率\(\mu \)の最大値はおよそ\(\mu _{\max }= \fbox {　 （イ） 　} \ \mathrm {H/m}\)であることが分かる。このとき，強磁性体の比透磁率はほぼ\(\mu _{\mathrm {r} }= \fbox {　 （ウ） 　}\)である。点\(\mathrm {P}\)以降は磁界に対する磁束密度の増加が次第に緩くなり，磁束密度はほぼ一定の値となる。この現象を\(\fbox {　 （エ） 　}\)という。

ただし，真空の透磁率を\(\mu _{0} =4\pi \times 10^{-7} \ \mathrm {H/m}\)とする。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 大きい & 7.5\times 10^{-3} & 6.0\times 10^{3} & 磁気飽和 \\
\hline
(2) & 小さい & 7.5\times 10^{-3} & 9.4\times 10^{-9} & 残留磁気 \\
\hline
(3) & 小さい & 1.5\times 10^{-2} & 9.4\times 10^{-9} & 磁気遮へい \\
\hline
(4) & 大きい & 7.5\times 10^{-3} & 1.2\times 10^{4} & 磁気飽和 \\
\hline
(5) & 大きい & 1.5\times 10^{-2} & 1.2\times 10^{4} & 残留磁気 \\
\hline
\end{array}
\]

【ワンポイント解説】

強磁性体の初期磁化特性に関する問題です。電気理論では一般に物体の透磁率は一定として扱いますが，強磁性体は本問で扱うように一定となりませんので覚えておいて下さい。

1.磁束密度\(B\)と磁界の強さ\(H\)の関係
透磁率を\(\mu \)とすると，磁束密度\(B\)と磁界の強さ\(H\)の関係は，
\[
B=\mu H
\] となります。

【解答】

解答：(1)
(ア)
強磁性体は透磁率\(\mu \)が非常に大きい物質で
\[
\mu =\mu _{\mathrm {r}} \mu _{0}
\] の関係があり，比透磁率\(\mu _{\mathrm {r} }\)も\(1\)より大きくなります。

(イ)
透磁率\(\mu \)は問題図の原点を通る直線であり，その最大値\(\mu _{\max }\)は\(H= 2\times 10^{2} \mathrm {[A/m]}\)，\(B =1.5 \mathrm {[T]}\)の時である。よって，\(\mu _{\max }\)は，
\[
\begin{eqnarray}
\mu _{\max } &=&\frac {1.5}{2\times 10^{2}} \\[ 5pt ] &=&0.75\times 10^{-2} \\[ 5pt ] &=&7.5\times 10^{-3} \mathrm {[H/m]}
\end{eqnarray}
\] と求められる。

(ウ)
\( \ \mu =\mu _{\mathrm {r}} \mu _{0} \ \)の関係より，
\[
\begin{eqnarray}
\mu _{\mathrm {r}} &=&\frac {\mu _{\max }}{\mu _{0}} \\[ 5pt ] &=&\frac {7.5\times 10^{-3}}{4\pi \times 10^{-7}} \\[ 5pt ] &≒&0.60 \times 10^{4}　→　6.0 \times 10^{3}
\end{eqnarray}
\] と求められる。

(エ)
図の点\(\mathrm {P}\)以降は磁界に対する磁束密度の増加が次第に緩くなり，磁束密度はほぼ一定の値となる現象を磁気飽和と言います。