《機械》〈情報伝送及び処理〉[R06下:問18]論理回路の真理値表及び出力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の論理回路について，(a)及び(b)の問に答えよ。

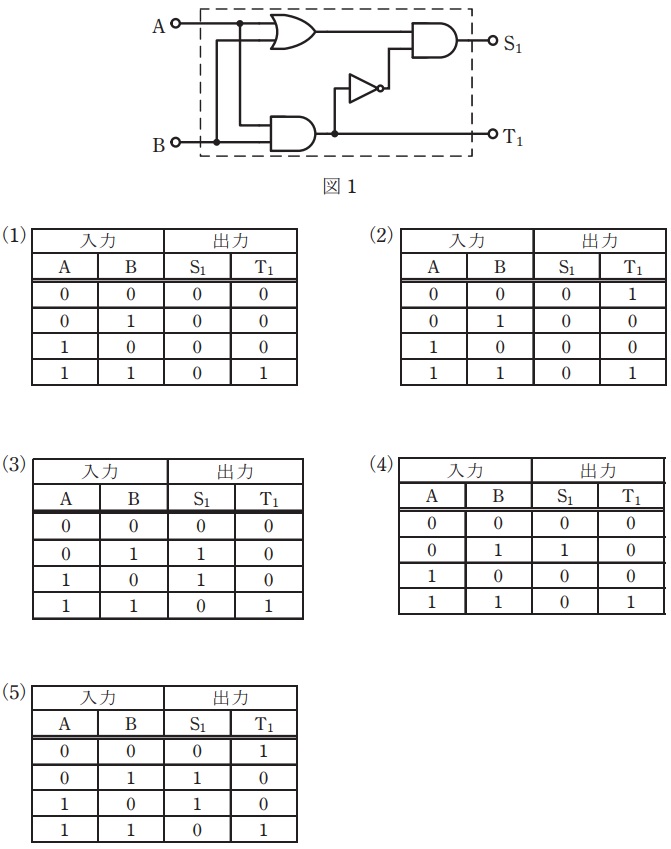
(a)　図1に示す論理回路の真理値表として，正しいものを次の(1)～(5)のうちから一つ選べ。

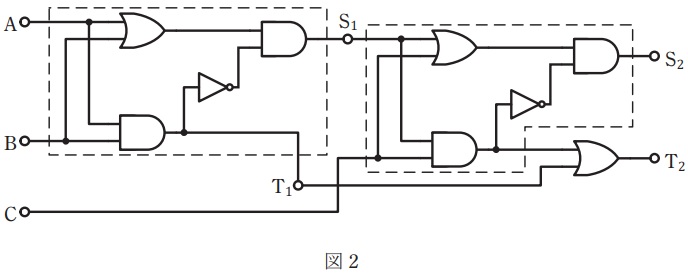
(b)　図1に示す論理回路を\( \ 2 \ \)組用いて図2に示すように接続して構成したとき，\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)の入力に対する出力\( \ \mathrm {S_{2}} \ \)及び\( \ \mathrm {T_{2}} \ \)の記述として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \mathrm {A=0} \ \)，\( \ \mathrm {B=0} \ \)，\( \ \mathrm {C=0} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=0} \ \)，\( \ \mathrm {T_{2}=1} \ \)である。

　(2)　\( \ \mathrm {A=0} \ \)，\( \ \mathrm {B=1} \ \)，\( \ \mathrm {C=0} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=1} \ \)，\( \ \mathrm {T_{2}=0} \ \)である。

　(3)　\( \ \mathrm {A=0} \ \)，\( \ \mathrm {B=0} \ \)，\( \ \mathrm {C=1} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=0} \ \)，\( \ \mathrm {T_{2}=1} \ \)である。

　(4)　\( \ \mathrm {A=1} \ \)，\( \ \mathrm {B=0} \ \)，\( \ \mathrm {C=1} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=1} \ \)，\( \ \mathrm {T_{2}=0} \ \)である。

　(5)　\( \ \mathrm {A=1} \ \)，\( \ \mathrm {B=1} \ \)，\( \ \mathrm {C=0} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=1} \ \)，\( \ \mathrm {T_{2}=1} \ \)である。

【ワンポイント解説】

ブロック線図から真理値表を導く問題です。
解法は複数ありますが，解答のように一つずつ信号を入れていくと確実かと思います。問14にも類題が出題されたので，真理値表を得意とされている方が有利な試験であった印象です。
本問は平成28年問18からの再出題となります。

1.主な論理回路の真理値表
基本的な論理回路と図記号は覚える必要がありますので，以下の真理値表を覚えておきましょう。

①\( \ \mathrm {AND} \ \)回路
論理積といい，すべての入力が\( \ 1 \ \)の時のみ\( \ 1 \ \)が出力される回路で，真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
　\mathrm {A}　 & 　\mathrm {B}　 & 　出力　 \\
\hline
0 & 0 & \color {blue }{0} \\
0 & 1 & \color {blue }{0} \\
1 & 0 & \color {blue }{0} \\
1 & 1 & \color {red}{1} \\
\end{array}
\]

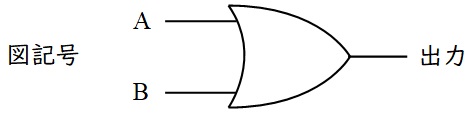
②\( \ \mathrm {OR} \ \)回路
論理和といい，入力が一つでも\( \ 1 \ \)の時\( \ 1 \ \)が出力される回路で，真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
　\mathrm {A}　 & 　\mathrm {B}　 & 　出力　 \\
\hline
0 & 0 & \color {blue }{0} \\
0 & 1 & \color {red}{1} \\
1 & 0 & \color {red}{1} \\
1 & 1 & \color {red}{1} \\
\end{array}
\]

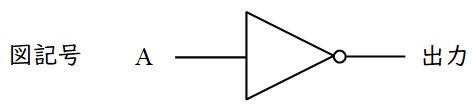
③\( \ \mathrm {NOT} \ \)回路
論理否定といい，入力を反転する回路で，真理値表と図記号は以下の通りです。
\[
\begin{array}{c|c}
　\mathrm {A}　 & 　出力　 \\
\hline
0 & \color {red}{1} \\
1 & \color {blue }{0} \\
\end{array}
\]

④\( \ \mathrm {NAND} \ \)回路
\( \ \mathrm {NOT}+\mathrm {AND} \ \)で\( \ \mathrm {AND} \ \)の\( \ \mathrm {NOT} \ \)を出力，すなわちすべての入力が\( \ 1 \ \)の時のみ\( \ 0 \ \)が出力される回路で，真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
　\mathrm {A}　 & 　\mathrm {B}　 & 　出力　 \\
\hline
0 & 0 & \color {red}{1} \\
0 & 1 & \color {red}{1} \\
1 & 0 & \color {red}{1} \\
1 & 1 & \color {blue }{0} \\
\end{array}
\]

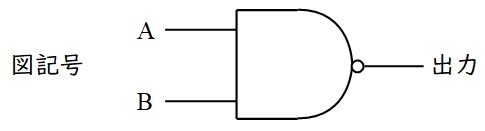
⑤\( \ \mathrm {NOR} \ \)回路
\( \ \mathrm {NOT}+\mathrm {OR} \ \)で\( \ \mathrm {OR} \ \)の\( \ \mathrm {NOT} \ \)を出力，すなわち入力が一つでも\( \ 1 \ \)の時\( \ 0 \ \)が出力される回路で，真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
　\mathrm {A}　 & 　\mathrm {B}　 & 　出力　 \\
\hline
0 & 0 & \color {red}{1} \\
0 & 1 & \color {blue }{0} \\
1 & 0 & \color {blue }{0} \\
1 & 1 & \color {blue }{0} \\
\end{array}
\]

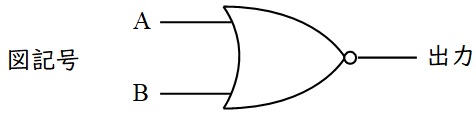
⑥\( \ \mathrm {ExOR} \ \)回路
排他的論理和\( \ \left( \mathrm {exclusive \ or} \right) \ \)といい，入力が異なるとき\( \ 1 \ \)，入力が同じ時\( \ 0 \ \)が出力される回路で，真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
　\mathrm {A}　 & 　\mathrm {B}　 & 　出力　 \\
\hline
0 & 0 & \color {blue }{0} \\
0 & 1 & \color {red}{1} \\
1 & 0 & \color {red}{1} \\
1 & 1 & \color {blue }{0} \\
\end{array}
\]

【解答】

(a)解答：(3)
ワンポイント解説「1.主な論理回路の真理値表」に沿って，図1に各入力信号を与えると図4のように出力される。したがって，真理値表として正しいのは(3)と求められる。

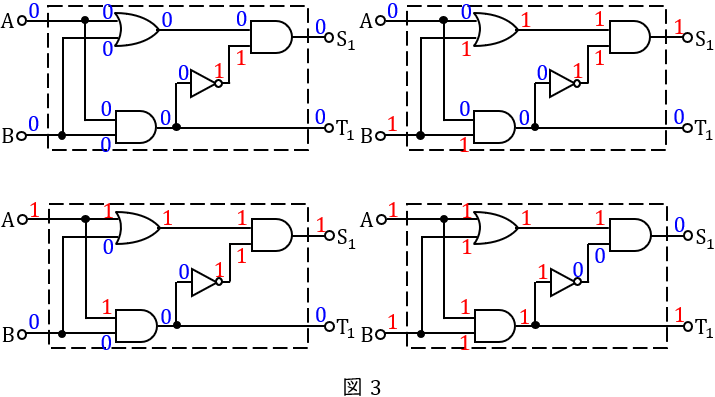
(b)解答：(2)
(a)の結果を利用して，(a)と同様に出力を求めると表1のようになります。

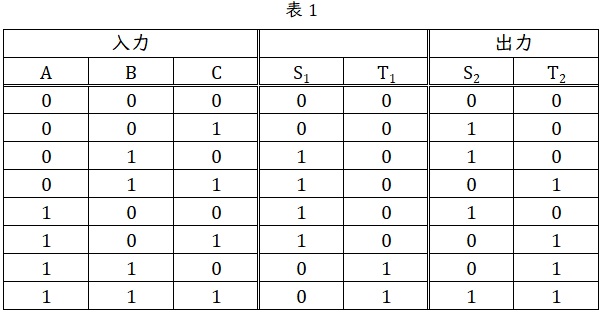
(1)誤り
表1の通り，\( \ \mathrm {A=0} \ \)，\( \ \mathrm {B=0} \ \)，\( \ \mathrm {C=0} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=0} \ \)，\( \ \mathrm {T_{2}=\color {red}{0}} \ \)となります。

(2)正しい
表1の通り，\( \ \mathrm {A=0} \ \)，\( \ \mathrm {B=1} \ \)，\( \ \mathrm {C=0} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=1} \ \)，\( \ \mathrm {T_{2}=0} \ \)となります。

(3)誤り
表1の通り，\( \ \mathrm {A=0} \ \)，\( \ \mathrm {B=0} \ \)，\( \ \mathrm {C=1} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=\color {red}{1}} \ \)，\( \ \mathrm {T_{2}=\color {red}{0}} \ \)となります。

(4)誤り
表1の通り，\( \ \mathrm {A=1} \ \)，\( \ \mathrm {B=0} \ \)，\( \ \mathrm {C=1} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=\color {red}{0}} \ \)，\( \ \mathrm {T_{2}=\color {red}{1}} \ \)となります。

(5)誤り
表1の通り，\( \ \mathrm {A=1} \ \)，\( \ \mathrm {B=1} \ \)，\( \ \mathrm {C=0} \ \)を入力したときの出力は，\( \ \mathrm {S_{2}=\color {red}{0}} \ \)，\( \ \mathrm {T_{2}=1} \ \)となります。