《機械》〈同期機〉[H19:問5]三相同期発電機の同期インピーダンスの導出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

定格速度，励磁電流\( \ 480 \ \mathrm {[A]} \ \)，無負荷で運転している三相同期発電機がある。この状態で，無負荷電圧（線間）を測ると\( \ 12 \ 600 \ \mathrm {[V]} \ \)であった。つぎに，\( \ 96 \ \mathrm {[A]} \ \)の励磁電流を流して短絡試験を実施したところ，短絡電流は\( \ 820 \ \mathrm {[A]} \ \)であった。この同期発電機の同期インピーダンス\( \ \mathrm {[\Omega ]} \ \)の値として，最も近いのは次のうちどれか。

ただし，磁気飽和は無視できるものとする。

　(1)　\( \ 1.77 \ \)　　(2)　\( \ 3.07 \ \)　　(3)　\( \ 15.4 \ \)　　(4)　\( \ 44.4 \ \)　　(5)　\( \ 76.8 \ \)

【ワンポイント解説】

三相同期発電機の同期インピーダンスの導出に関する問題です。
計算量はそれほど多くありませんが，等価回路も特性曲線も与えられていないので，自分自身で考えて解いていく必要があります。さらに，相電圧か線間電圧のどちらを採用しなければならないかも理解していなければ解けない問題です。

1.同期発電機の等価回路
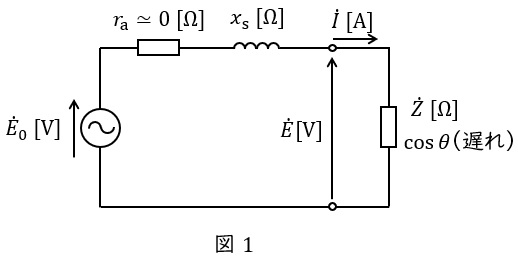
同期発電機の一相分等価回路は誘導起電力（相電圧）\( \ {\dot E}_{0} \ \mathrm {[V]} \ \)，端子電圧（相電圧）\( \ \dot E \ \mathrm {[V]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。
通常，電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え，無視して考えることが一般的です。
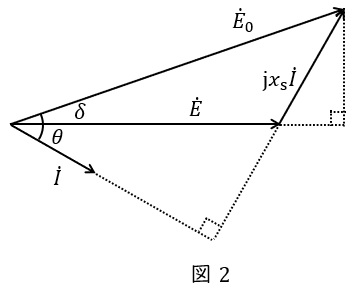
また，等価回路よりベクトル図は図2のようになります。ただし，\( \ \theta \ \)は力率角，\( \ \delta \ \)は負荷角です。

2.同期発電機の無負荷飽和曲線と三相短絡曲線
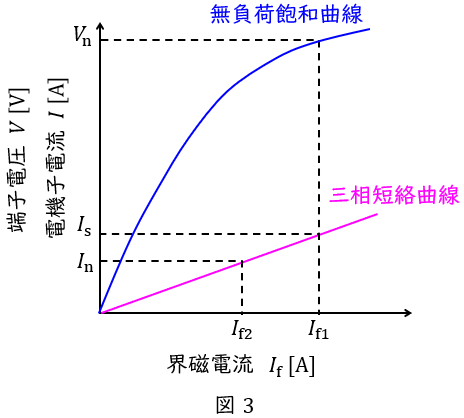
同期発電機は図3のような無負荷飽和曲線と三相短絡曲線の特性があります。
無負荷飽和曲線は定格速度で無負荷で運転したときの界磁電流と端子電圧の関係，三相短絡曲線は電機子巻線の三相の出力端子を短絡し定格速度で運転したときの界磁電流と三相短絡電流の関係，を表したものです。
図中の\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
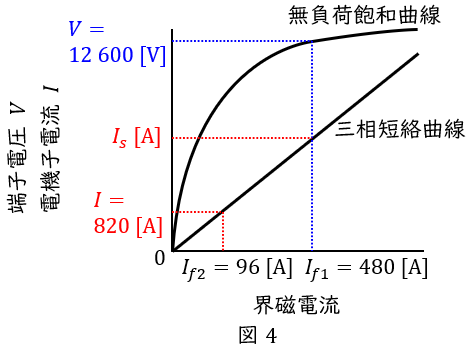
題意に沿って，本問における無負荷飽和曲線と三相短絡曲線上の関係を図示すると図4のようになる。図4より，\( \ V=12 \ 600 \ \mathrm {[V]} \ \)における短絡電流\( \ I_{s} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{s} &=& \frac {I_{f1}}{I_{f2}}I \\[ 5pt ] &=& \frac {480}{96}\times 820 \\[ 5pt ] &=& 4 \ 100 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。

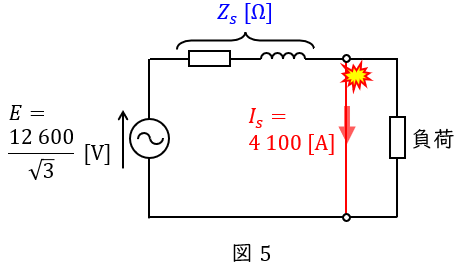
ワンポイント解説「1.同期発電機の等価回路」から，三相短絡時の等価回路は図5のようになり，同期インピーダンス\( \ Z_{s} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
Z_{s} &=& \frac {E}{I_{s}} \\[ 5pt ] &=& \frac {\displaystyle \frac {12 \ 600}{\sqrt {3}}}{4 \ 100} \\[ 5pt ] &≒& 1.77 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。