《機械》〈情報伝送及び処理〉[H27:問14]論理回路の論理式の導出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

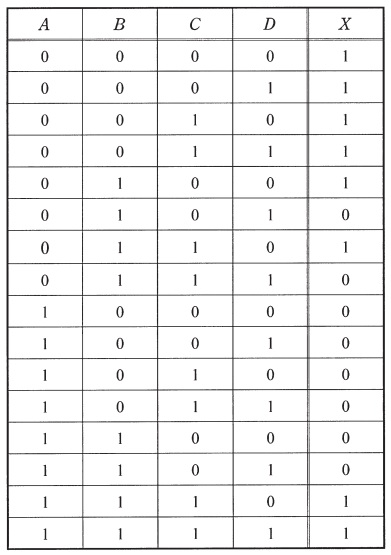
次の真理値表の出力を表す論理式として，正しい式を次の(1)～(5)のうちから一つ選べ。

　　　　

(1)　\(X=\overline A \cdot \overline B + \overline A \cdot \overline D +B\cdot C \cdot D\)　　(2)　\(X=\overline A \cdot B + \overline A \cdot \overline D +A\cdot B \cdot C\)
(3)　\(X=\overline A \cdot \overline B + \overline A \cdot \overline D +A\cdot B \cdot C\)　　(4)　\(X=\overline A \cdot \overline B + \overline A \cdot \overline C +B\cdot C \cdot D\)
(5)　\(X=\overline A \cdot \overline B + \overline A \cdot \overline C +A\cdot B \cdot D\)

【ワンポイント解説】

専門の方であれば，ある程度基本問題に近い内容ですが，電験受験者のほとんどの方は本問の専門外であると思います。カルノー図で解く方法とブール代数で解く方法があります。ルールをいろいろ記載していますが，慣れの面が強いので，問題演習を通じて理解するようにして下さい。

1.カルノー図
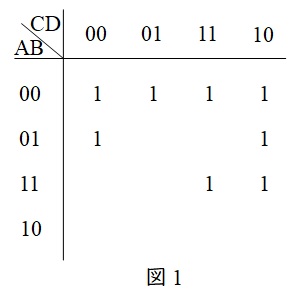
図1のように，真理値表を整理して，ブール代数を簡略化して解く方法です。カルノー図を使用する際，以下のルールがあります。
・\( \ 00 \ \)，\( \ 01 \ \)，\( \ 11 \ \)，\( \ 10 \ \)の順に描く。
・\( \ 0 \ \)を書かず，\( \ 1 \ \)のみを記載する。
・なるべく大きな長方形で囲い，式を整理する。
・一番上と一番下及び一番左と一番右は繋がっていると考える。

2.ブール代数の法則
以下の法則は覚えるのではなく，高校生の数学で習った集合の内容を思い出し，頭でイメージするようにして下さい。
①恒等則
　\(1+A=1\)，\(0\cdot A=0\)，\(0+A=A\)，\(1\cdot A =A\)

②べき等則
　\(A+A=A\)，\(A\cdot A=A\)

③補元則
　\(A\cdot \overline A=0\)，\(A +\overline A=1\)

④二重否定
　\(\overline {\overline A}=A\)

⑤交換則
　\(A+B=B+A\)，\(A\cdot B =B\cdot A\)

⑥結合則
　\(A+(B+C)=(A+B)+C\)，\(A\cdot (B\cdot C)=(A\cdot B)\cdot C\)

⑦分配則
　\(A\cdot (B+C)=A\cdot B +A\cdot C\)，\(A+(B\cdot C)=(A+B)\cdot (A+C)\)

⑧吸収則
　\(A\cdot (A+B)=A\)，\(A+A\cdot B=A\)

⑨ド・モルガンの定理
　\(\overline {A+B}=\overline A \cdot \overline B\)，\(\overline {A\cdot B}=\overline A +\overline B\)

【解答】

解答：(3)
問題の真理値表をカルノー図に描くとワンポイント解説の図1のようになるから，カルノー図のルールに従って四角形で囲うと図2のようになる。

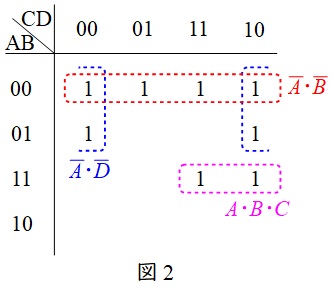
図2より，
\[
\begin{eqnarray}
X&=&\overline A \cdot \overline B +\overline A \cdot \overline D +A\cdot B\cdot C \\[ 5pt ] \end{eqnarray}
\] と求められる。