《理論》〈電気回路〉[H26:問15]交流回路の電力計算に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，正弦波交流電圧\(E \ \mathrm {[V]}\)の電源が誘導性リアクタンス\(X \ \mathrm {[\Omega ]}\)のコイルと抵抗\(R \ \mathrm {[\Omega ]}\)との並列回路に電力を供給している。この回路において，電流計の指示値は\(12.5 \ \mathrm {A}\)，電圧計の指示値は\(300 \ \mathrm {V}\)，電力計の指示値は\(2250 \ \mathrm {W}\)であった。

ただし，電圧計，電流計及び電力計の損失はいずれも無視できるものとする。次の(a)及び(b)の問に答えよ。

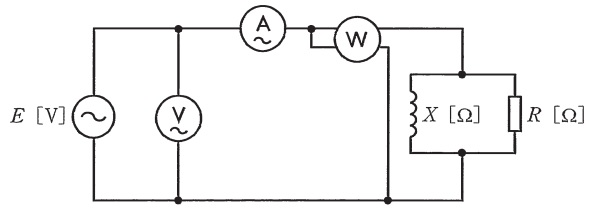
(a)　この回路における無効電力\(Q \ \mathrm {[var ]}\)として，最も近い\(Q\)の値を次の(1)～(5)のうちから一つ選べ。

　(1)　\(1800\)　　(2)　\(2250\)　　(3)　\(2750\)　　(4)　\(3000\)　　(5)　\(3750\)

(b)　誘導性リアクタンス\(X \ \mathrm {[\Omega ]}\)として，最も近い\(X\)の値を次の(1)～(5)のうちから一つ選べ。

　(1)　\(16\)　　(2)　\(24\)　　(3)　\(30\)　　(4)　\(40\)　　(5)　\(48\)

【ワンポイント解説】

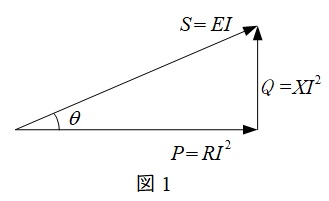
交流の問題は下図のようなベクトル図を描くことが重要です。電験では遅れ無効電力を正とする場合が多いので，図1のように，普段からリアクトルの場合は無効電力は正側に描いた方が良いでしょう。

【解答】

(a)解答：(4)
この回路の皮相電力\(S \ \mathrm {[V\cdot A ]}\)は，
\[
\begin{eqnarray}
S &=&VI \\[ 5pt ] &=&300\times 12.5 \\[ 5pt ] &=&3750 \ \mathrm {[V\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となる。図1より，有効電力\(P\)が\(2250 \ \mathrm {W}\)であるので，無効電力\(Q \ \mathrm {[var ]}\)の大きさは，
\[
\begin{eqnarray}
Q &=&\sqrt {S^{2}-P^{2}} \\[ 5pt ] &=&\sqrt {3750^{2}-2250^{2}} \\[ 5pt ] &=&3000 \ \mathrm {[var]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
リアクトルにかかる電圧は\(300 \ \mathrm {V}\)であるから，無効電力\(Q\)との関係より，
\[
\begin{eqnarray}
Q &=&\frac {V^{2}}{X} \\[ 5pt ] X&=&\frac {V^{2}}{Q} \\[ 5pt ] &=&\frac {300^{2}}{3000} \\[ 5pt ] &=&30 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。