《理論》〈電気回路〉[H25:問12]RL直並列回路の過渡現象に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

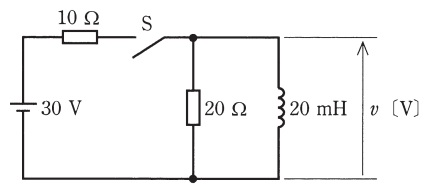
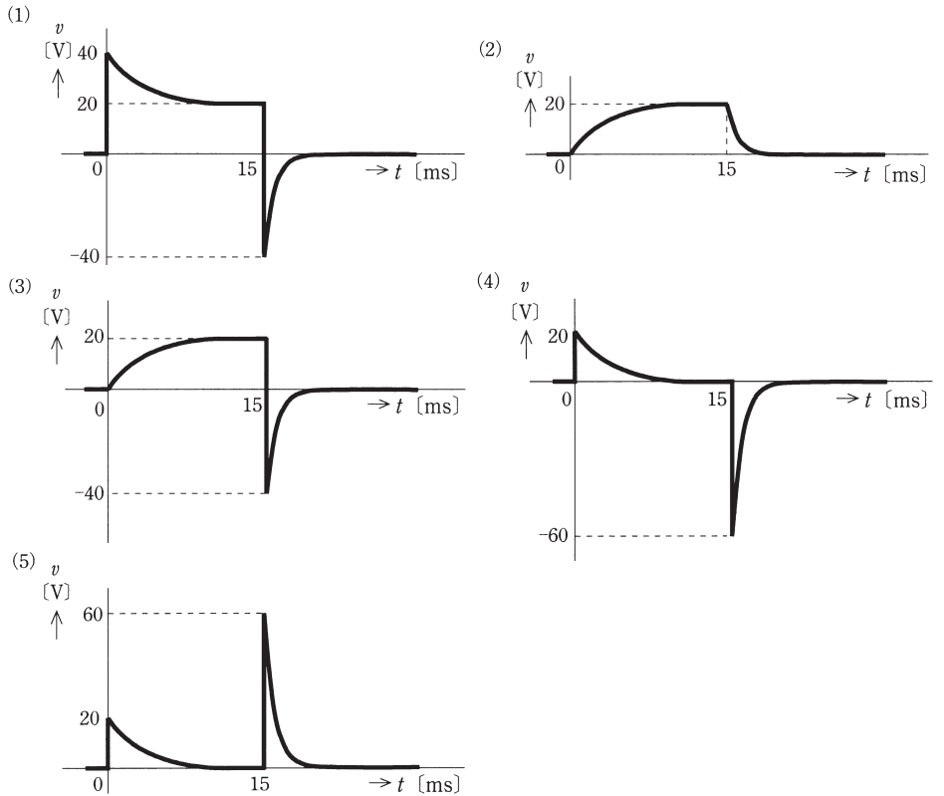
図の回路において，十分に長い時間開いていたスイッチ$\ \mathrm {S} \ $を時刻$\ t=0 \ \mathrm {[ms]} \ $から時刻$\ t=15 \ \mathrm {[ms]} \ $の間だけ閉じた。このとき，インダクタンス$\ 20 \ \mathrm {[mH]} \ $のコイルの端子間電圧$\ v \ \mathrm {[V]} \ $の時間変化を示す図として，最も近いものを次の(1)～(5)のうちから一つ選べ。

【ワンポイント解説】

過渡現象に関する問題です。過渡現象におけるリアクトルの過渡状態と定常状態がどうなるかを理解しておくようにしておきましょう。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

【関連する「電気の神髄」記事】

RL並列回路の過渡現象（直流回路）

【解答】

解答：(4)
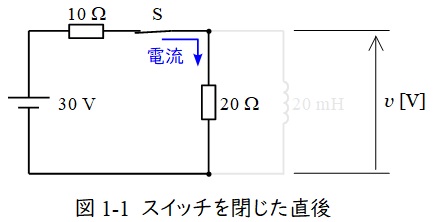
ワンポイント解説「1.過渡現象におけるリアクトルの過渡状態と定常状態」スイッチを入れた直後はリアクトルは開放していると考えるので，回路は図1-1のように考える。
図1-1より，$\ v \ \mathrm {[V]} \ $は$\ 20 \ \mathrm {[\Omega ]} \ $の抵抗の両端の電圧となるから，
$$\begin{eqnarray} v &=&\frac {20}{10+20}\times 30 \\[ 5pt ] &=&20 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ となる。

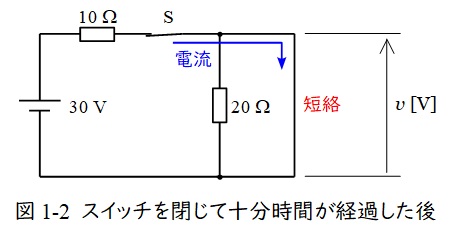
スイッチを入れて十分経過した後は，リアクトルは短絡と考えれば良いから，回路は図1-2の通りとなる。
よって，$\ v=0 \ \mathrm {[V]} \ $となり，この時リアクトルを流れる電流$\ I \ \mathrm {[A]} \ $は，
$$\begin{eqnarray} I &=&\frac {30}{10} \\[ 5pt ] &=&3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ となる。

スイッチを入れて十分経過した後，スイッチを再び開くと，リアクトルは流れる電流値を維持しようとする働きをする。したがって，回路は図2-1のようになり，電流は$\ 3 \ \mathrm {A} \ $流れ続けることになる。したがって，$\ v \ \mathrm {[V]} \ $は抵抗での電圧降下と等しくなり，電圧の向きに注意すると，
$$\begin{eqnarray} v &=&-3\times 20 \\[ 5pt ] &=&-60 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ となる。

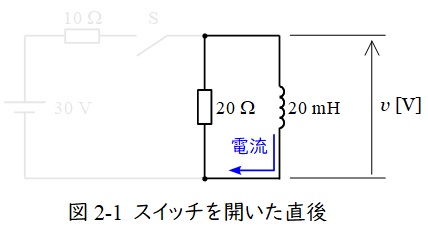
スイッチを開いて十分経過すると，リアクトルに蓄えられているエネルギーが放出され，回路には電流が流れなくなる。したがって，$\ v=0 \ \mathrm {[V]} \ $となる。

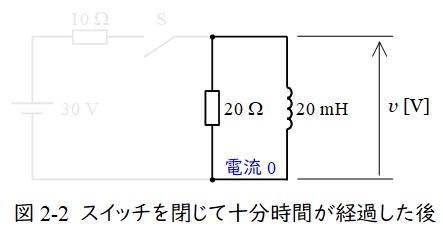
以上から，コイルの端子間電圧$\ v \ \mathrm {[V]} \ $の時間変化は(4)となる。