《機械》〈電熱〉[R2:問13]熱の伝導と電気の伝導の対応表に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

熱の伝導は電気の伝導によく似ている。下記は，電気系の量と熱系の量の対応表である。

　　　　　　　　　　　　電気系と熱系の対応表
\[
\begin{array}{|c|c|}
\hline
電気系の量 & 熱系の量 \\[ 5pt ] \hline
電圧 \ V \ \mathrm {[V]} & \fbox {　 （ア） 　} \ \mathrm {[K]} \\[ 5pt ] \hline
電気量 \ Q \ \mathrm {[C]} & 熱量 \ Q \ \mathrm {[J]} \\[ 5pt ] \hline
電流 \ I \ \mathrm {[A]} & \fbox {　 （イ） 　} \ \mathrm {[W]} \\[ 5pt ] \hline
　　　導電率 \ \sigma \ \mathrm {[S/m]}　　　 & 　熱伝導率 \ \lambda \ \mathrm {[W／\left( m\cdot K\right) ]}　 \\[ 5pt ] \hline
電気抵抗 \ R \ \mathrm {[\Omega ]} & 熱抵抗 \ R_{\mathrm {T}} \ \fbox {　 （ウ） 　} \\[ 5pt ] \hline
静電容量 \ C \ \mathrm {[F]} & 熱容量 \ C \ \fbox {　 （エ） 　} \\[ 5pt ] \hline
\end{array}
\]

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　熱流 \ \mathit {\Phi}　 & 　温度差 \ \theta　 & 　\mathrm {[J/K]}　 & 　\mathrm {[K/W]}　 \\
\hline
(2) & 　温度差 \ \theta　 & 　熱流 \ \mathit {\Phi}　 & 　\mathrm {[K/W]}　 & 　\mathrm {[J/K]}　 \\
\hline
(3) & 　温度差 \ \theta　 & 　熱流 \ \mathit {\Phi}　 & 　\mathrm {[K/J]}　 & 　\mathrm {[J/K]}　 \\
\hline
(4) & 　熱流 \ \mathit {\Phi}　 & 　温度差 \ \theta　 & 　\mathrm {[J/K]}　 & 　\mathrm {[J/W]}　 \\
\hline
(5) & 　温度差 \ \theta　 & 　熱流 \ \mathit {\Phi}　 & 　\mathrm {[K/W]}　 & 　\mathrm {[J/W]}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

（ア）の単位\( \ \mathrm {[K]} \ \)は絶対温度の単位で，摂氏の\( \ \mathrm {[℃]} \ \)に\( \ 273.15 \ \)を足した数値です。
理論科目の電磁気や電気回路の公式を覚えていれば，対応させるだけで解けると思います。

1.熱力学におけるオームの法則
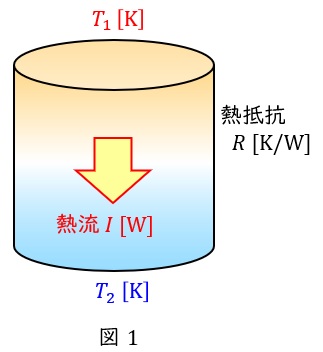
図1に示すように，ある温度差がある物体においては高温部から低温部に向かい熱が伝わり，それを熱流といいます。
物体の温度差を\( \ \theta =T_{1}-T_{2} \ \mathrm {[K]} \ \)，熱抵抗を\( \ R \ \mathrm {[K / W]} \ \)とすると，物体の熱流\( \ I \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
I &=& \frac {\theta }{R} \\[ 5pt ] \end{eqnarray}
\] となります。

2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)
物体の熱伝導率が\( \ \lambda \ \mathrm {[W / (m\cdot K )]} \ \)，断面積が\( \ S \ \mathrm {[m^{2}]} \ \)，長さが\( \ l \ \mathrm {[m]} \ \)であるとき，物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は，
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
(ア)
ワンポイント解説「1.熱力学におけるオームの法則」の通り，電気系の電圧（電位差）に対応するのは，温度差\( \ \theta \ \)です。単位の\( \ \mathrm {[K]} \ \)がヒントになっています。

(イ)
ワンポイント解説「1.熱力学におけるオームの法則」の通り，電気系の電流に対応するのは，熱流\( \ \ \mathit {\Phi} \ \)です。名称も似ているので，イメージもしやすいと思います。

(ウ)
ワンポイント解説「1.熱力学におけるオームの法則」の通り，オームの法則において，
\[
\begin{eqnarray}
R \ \mathrm {[\Omega ]}&=&\frac {V \ \mathrm {[V]}}{I \ \mathrm {[A]}} \\[ 5pt ] \end{eqnarray}
\] となるので，これに対応する単位は，
\[
\begin{eqnarray}
R_{\mathrm {T}}&=&\frac {\theta \ \mathrm {[K]}}{\mathit {\Phi} \ \mathrm {[W]}}　→　\mathrm {[K／W]} \\[ 5pt ] \end{eqnarray}
\] となります。

(エ)
静電容量\( \ C \ \mathrm {[F]} \ \)は，
\[
\begin{eqnarray}
C \ \mathrm {[F]}&=&\frac {Q \ \mathrm {[C]}}{V \ \mathrm {[V]}} \\[ 5pt ] \end{eqnarray}
\] となるので，これに対応する単位は，
\[
\begin{eqnarray}
C&=&\frac {Q \ \mathrm {[J]}}{\theta \ \mathrm {[K]}}　→　\mathrm {[J／K]} \\[ 5pt ] \end{eqnarray}
\] となります。