【問題】
【難易度】★★★☆☆(普通)
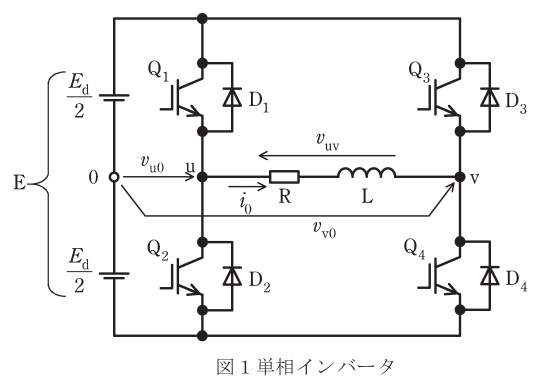
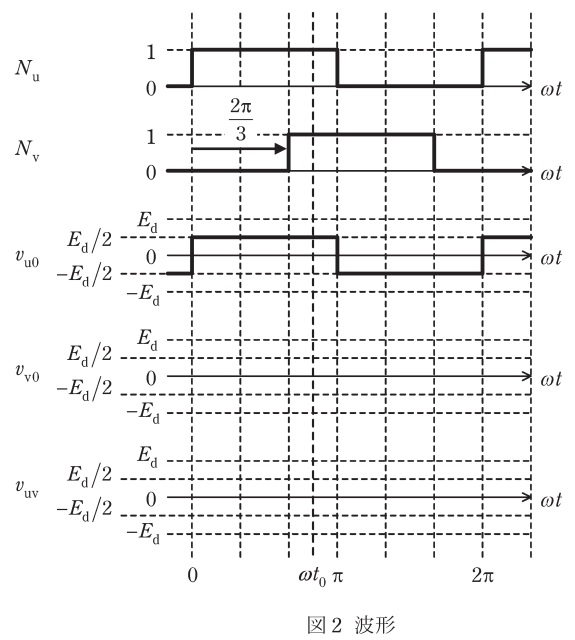
図1は直流電圧\( \ E_{\mathrm {d}} \ \)(直流電源\( \ \mathrm {E} \ \))の単相インバータに誘導性負荷を接続した回路を示す。また,図2には,\( \ \displaystyle \frac {2\pi }{3} \ \)の位相差がある\( \ \mathrm {u} \ \),\( \ \mathrm {v} \ \)相のノッチ波\( \ N_{\mathrm {u}} \ \)と\( \ N_{\mathrm {v}} \ \)と,直流中間電圧点\( \ 0 \ \)と出力端子\( \ \mathrm {u} \ \)との間の\( \ \mathrm {u} \ \)相電圧\( \ v_{\mathrm {u0}} \ \)の波形を示す。ノッチ波は,上アームにオン信号を与えるときに\( \ 1 \ \),下アームにオン信号を与えるときに\( \ 0 \ \)とする。このインバータの動作に関して,次の問に答えよ。
(1) 図2に示す位相\( \ \omega t_{\mathrm {0}} \ \)において,スイッチングデバイス\( \ \mathrm {Q}_{\mathrm {1}} \ \),\( \ \mathrm {Q}_{\mathrm {2}} \ \),\( \ \mathrm {Q}_{\mathrm {3}} \ \)及び\( \ \mathrm {Q}_{\mathrm {4}} \ \)のうち,オン信号が与えられているデバイスを答えよ。
(2) 図2が答案用紙にも示されている。電圧が変化するタイミングと電圧の大きさが明確に分かるように,上から\( \ 4 \ \)段目には\( \ \mathrm {v} \ \)相電圧\( \ v_{\mathrm {v0}} \ \)を,最下段には負荷電圧\( \ v_{\mathrm {uv}} \ \)の波形を答案用紙に示せ。
(3) 小問(2)の運転において,負荷は誘導性であるので,負荷電圧\( \ v_{\mathrm {uv}} \ \)が零になった直後も負荷電流\( \ i_{\mathrm {0}} \ \)はすぐに零にならず,それ以前の電流の方向に流れ続ける。\( \ i_{\mathrm {0}}>0 \ \)で,\( \ v_{\mathrm {uv}} \ \)が零になった直後に継続する電流の経路はどのようになるか。例えば\( \ \mathrm {L}-\mathrm {D}_{3}-\mathrm {E}-\mathrm {D}_{2}-\mathrm {R}-\mathrm {L} \ \)のように\( \ \mathrm {L} \ \)を起点,終点とする回路要素を結んだループで,経路を示せ。同様に\( \ i_{\mathrm {0}}<0 \ \)で\( \ v_{\mathrm {uv}} \ \)が零になった直後に継続する電流はどのような経路になるかを示せ。ただし,各回路要素は,負荷インダクタを\( \ \mathrm {L} \ \),負荷抵抗を\( \ \mathrm {R} \ \),スイッチングデバイスを\( \ \mathrm {Q}_{\mathrm {1}}~\mathrm {Q}_{\mathrm {4}} \ \),ダイオードを\( \ \mathrm {D}_{\mathrm {1}}~\mathrm {D}_{\mathrm {4}} \ \),直流電源を\( \ \mathrm {E} \ \)とする。
(4) 図2に示す電圧\( \ v_{\mathrm {u0}} \ \)は方形波電圧であり,この波形をフーリエ級数展開すると\( \ \displaystyle v_{\mathrm {u0}}=\frac {4}{\pi }\cdot \frac {E_{\mathrm {d}}}{2}\displaystyle \sum_{n=1}^{\infty } \frac {\sin \left[ \left( 2n-1\right) \omega t \right] }{2n-1} \ \)と表される。\( \ v_{\mathrm {u0}} \ \)に含まれる基本波成分の瞬時値\( \ v_{\mathrm {u0f}}\left( \omega t \right) \ \)を\( \ E_{\mathrm {d}} \ \),関数\( \ \sin \ \)及び角周波数\( \ \omega \ \)を用いた式で示せ。
(5) 負荷電圧\( \ v_{\mathrm {uv}} \ \)は\( \ v_{\mathrm {uv}}=v_{\mathrm {u0}}-v_{\mathrm {v0}} \ \)である。\( \ v_{\mathrm {uv}} \ \)に含まれる基本波成分の瞬時値\( \ v_{\mathrm {uvf}}\left( \omega t \right) \ \)を\( \ E_{\mathrm {d}} \ \),関数\( \ \sin \ \)及び角周波数\( \ \omega \ \)を用いた式で示せ。また,その実効値\( \ V_{\mathrm {uvf}} \ \)は\( \ E_{\mathrm {d}} \ \)の何倍となるか,その値を示せ。
【ワンポイント解説】
単相インバータの動作に関する問題です。
(5)で少し計算量が多い内容が含まれますが,(1)~(4)は比較的取り組みやすく速く解ける内容となっているため,部分点狙いならば選択しても良いかなという印象の問題です。
1.三角関数の和積の公式
三角関数の加法定理は,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) &=&\sin \alpha \cos \beta +\cos \alpha \sin \beta &・・・・①& \\[ 5pt ]
\sin \left( \alpha – \beta \right) &=&\sin \alpha \cos \beta -\cos \alpha \sin \beta &・・・・②& \\[ 5pt ]
\cos \left( \alpha + \beta \right) &=&\cos \alpha \cos \beta -\sin \alpha \sin \beta &・・・・③& \\[ 5pt ]
\cos \left( \alpha – \beta \right) &=&\cos \alpha \cos \beta +\sin \alpha \sin \beta &・・・・④& \\[ 5pt ]
\end{eqnarray}
\]
であるから,\(①+②\)より,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) +\sin \left( \alpha – \beta \right) &=&2\sin \alpha \cos \beta &・・・・⑤& \\[ 5pt ]
\end{eqnarray}
\]
\(①-②\)より,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) -\sin \left( \alpha – \beta \right) &=&2\cos \alpha \sin \beta &・・・・⑥& \\[ 5pt ]
\end{eqnarray}
\]
\(③+④\)より,
\[
\begin{eqnarray}
\cos \left( \alpha + \beta \right) +\cos \left( \alpha – \beta \right) &=&2\cos \alpha \cos \beta &・・・・⑦& \\[ 5pt ]
\end{eqnarray}
\]
\(③-④\)より,
\[
\begin{eqnarray}
\cos \left( \alpha + \beta \right) -\cos \left( \alpha – \beta \right) &=&-2\sin \alpha \sin \beta &・・・・⑧& \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ \alpha + \beta =A \ \),\( \ \alpha – \beta =B \ \)とすると,\( \ \displaystyle \alpha =\frac {A+B}{2} \ \),\( \ \displaystyle \beta =\frac {A-B}{2} \ \)であるから,\( \ ⑤~⑧ \ \)に代入すると,
\[
\begin{eqnarray}
\sin A +\sin B &=&2\sin \frac {A+B}{2} \cos \frac {A-B}{2} \\[ 5pt ]
\sin A -\sin B &=&2\cos \frac {A+B}{2} \sin \frac {A-B}{2} \\[ 5pt ]
\cos A +\cos B &=&2\cos \frac {A+B}{2} \cos \frac {A-B}{2} \\[ 5pt ]
\cos A -\cos B &=&-2\sin \frac {A+B}{2} \sin \frac {A-B}{2} \\[ 5pt ]
\end{eqnarray}
\]
と和積の公式が求められます。
【関連する「電気の神髄」記事】
単相電圧形フルブリッジインバータ
さまざまな交流波形のフーリエ級数展開まとめ
【解答】
(1)図2に示す位相\( \ \omega t_{\mathrm {0}} \ \)において,オン信号が与えられているデバイス
位相\( \ \omega t_{\mathrm {0}} \ \)において,\( \ N_{\mathrm {u}} \ \)と\( \ N_{\mathrm {v}} \ \)はともに\( \ 1 \ \)であり,題意より「ノッチ波は,上アームにオン信号を与えるときに\( \ 1 \ \),下アームにオン信号を与えるときに\( \ 0 \ \)とする」ので,どちらも上アームがオンとなる。
したがって,オン信号が与えられているデバイスは\( \ \mathrm {Q}_{\mathrm {1}} \ \)と\( \ \mathrm {Q}_{\mathrm {3}} \ \)である。
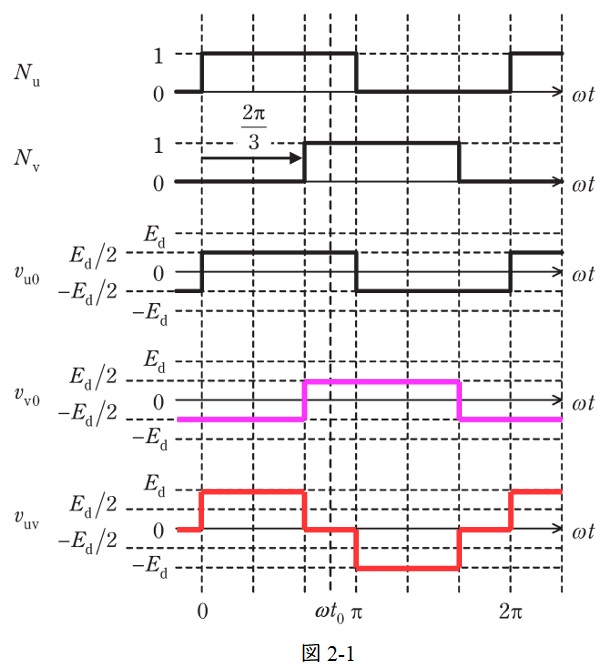
(2)\( \ \mathrm {v} \ \)相電圧\( \ v_{\mathrm {v0}} \ \)と負荷電圧\( \ v_{\mathrm {uv}} \ \)の波形
\( \ \mathrm {v} \ \)相電圧\( \ v_{\mathrm {v0}} \ \)は,\( \ N_{\mathrm {v}} \ \)が\( \ 1 \ \)のとき\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \),\( \ N_{\mathrm {v}} \ \)が\( \ 0 \ \)のとき\( \ \displaystyle -\frac {E_{\mathrm {d}}}{2} \ \)であり,負荷電圧\( \ v_{\mathrm {uv}} \ \)は,\( \ v_{\mathrm {uv}}=v_{\mathrm {u0}}-v_{\mathrm {v0}} \ \)なので,図2-1のように求められる。
(3)\( \ v_{\mathrm {uv}} \ \)が零になった直後に継続する電流の経路
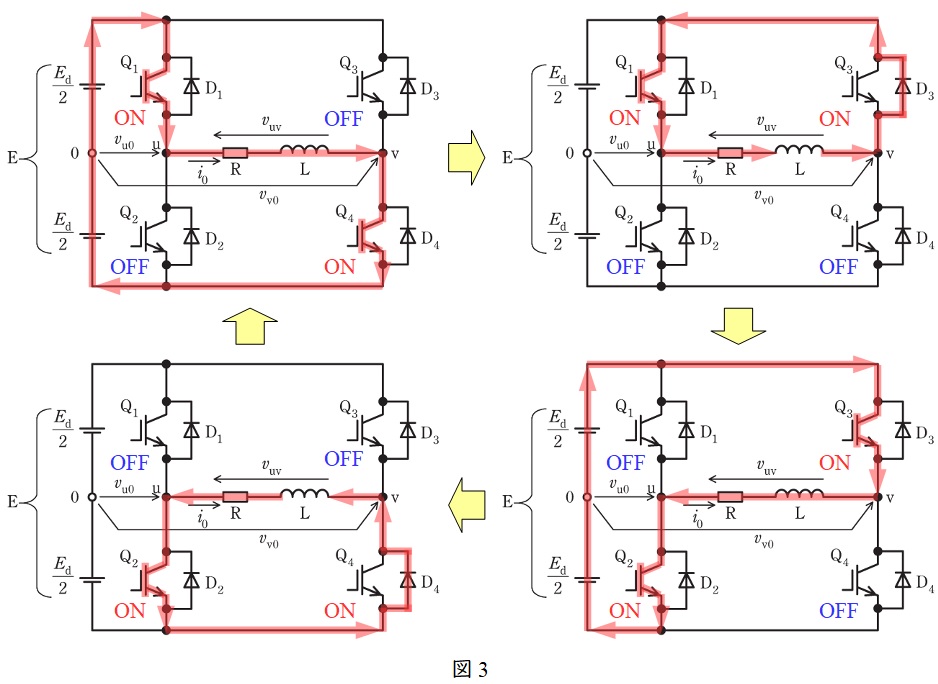
単相インバータの動作に沿って,図1の単相インバータを流れる電流の状態を示すと図3のようになる。
\( \ \displaystyle 0≦\omega t≦\frac {2}{3}\pi \ \)においては,\( \ \mathrm {Q}_{\mathrm {1}} \ \)と\( \ \mathrm {Q}_{\mathrm {4}} \ \)がオンであるので図3左上のように流れる。
\( \ \displaystyle \frac {2}{3}\pi≦\omega t≦\pi \ \)においては,\( \ \mathrm {Q}_{\mathrm {1}} \ \)と\( \ \mathrm {Q}_{\mathrm {3}} \ \)がオンであるので図3右上のようになり,リアクトルに蓄えられているエネルギーが放出され\( \ \mathrm {Q}_{\mathrm {3}} \ \)は還流ダイオード\( \ \mathrm {D}_{\mathrm {3}} \ \)を流れる。
\( \ \displaystyle \pi≦\omega t≦\frac {5}{3}\pi \ \)においては,\( \ \mathrm {Q}_{\mathrm {2}} \ \)と\( \ \mathrm {Q}_{\mathrm {3}} \ \)がオンであるので図3右下のように流れる。
\( \ \displaystyle \frac {5}{3}\pi≦\omega t≦2\pi \ \)においては,\( \ \mathrm {Q}_{\mathrm {2}} \ \)と\( \ \mathrm {Q}_{\mathrm {4}} \ \)がオンであるので図3左下のようになり,リアクトルに蓄えられているエネルギーが放出され\( \ \mathrm {Q}_{\mathrm {4}} \ \)は還流ダイオード\( \ \mathrm {D}_{\mathrm {4}} \ \)を流れる。
以後,これを繰り返す。
したがって,\( \ i_{\mathrm {0}}>0 \ \)で,\( \ v_{\mathrm {uv}} \ \)が零になった直後に継続する電流の経路は図3の右上の経路となり,\( \ \mathrm {L- D_{\mathrm {3}} - Q_{\mathrm {1}} -R-L} \ \)と求められる。
同様に,\( \ i_{\mathrm {0}}<0 \ \)で\( \ v_{\mathrm {uv}} \ \)が零になった直後に継続する電流の経路は図3の左下の経路となり,\( \ \mathrm {L-R - Q_{\mathrm {2}}- D_{\mathrm {4}} -L} \ \)と求められる。
(4)\( \ v_{\mathrm {u0}} \ \)に含まれる基本波成分の瞬時値\( \ v_{\mathrm {u0f}}\left( \omega t \right) \ \)を示す
\( \ v_{\mathrm {u0}} \ \)に含まれる基本波成分の瞬時値\( \ v_{\mathrm {u0f}}\left( \omega t \right) \ \)は,\( \ \displaystyle v_{\mathrm {u0}}=\frac {4}{\pi }\cdot \frac {E_{\mathrm {d}}}{2}\displaystyle \sum_{n=1}^{\infty } \frac {\sin \left[ \left( 2n-1\right) \omega t\right] }{2n-1} \ \)に\( \ n=1 \ \)を代入すると,
\[
\begin{eqnarray}
v_{\mathrm {u0f}}\left( \omega t \right) &=&\frac {4}{\pi }\cdot \frac {E_{\mathrm {d}}}{2}\cdot \frac {\sin \left[ \left( 2\times 1-1\right) \omega t\right] }{2\times 1-1} \\[ 5pt ]
&=&\frac {4}{\pi }\cdot \frac {E_{\mathrm {d}}}{2}\sin \omega t \\[ 5pt ]
&=&\frac {2E_{\mathrm {d}}}{\pi }\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ v_{\mathrm {uv}} \ \)に含まれる基本波成分の瞬時値\( \ v_{\mathrm {uvf}}\left( \omega t \right) \ \)と実効値\( \ V_{\mathrm {uvf}} \ \)
負荷電圧\( \ v_{\mathrm {uv}} \ \)は\( \ v_{\mathrm {uv}}=v_{\mathrm {u0}}-v_{\mathrm {v0}} \ \)であり,\( \ v_{\mathrm {v0}} \ \)は\( \ v_{\mathrm {u0}} \ \)から\( \ \displaystyle \frac {2}{3}\pi \ \)遅れた波形であるから,\( \ v_{\mathrm {uv}} \ \)に含まれる基本波成分の瞬時値\( \ v_{\mathrm {uvf}}\left( \omega t \right) \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {uvf}}\left( \omega t \right) &=&v_{\mathrm {u0f}}\left( \omega t \right) -v_{\mathrm {v0f}}\left( \omega t \right) \\[ 5pt ]
&=&\frac {2E_{\mathrm {d}}}{\pi }\sin \omega t -\frac {2E_{\mathrm {d}}}{\pi }\sin \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ]
&=&\frac {2E_{\mathrm {d}}}{\pi }\left\{ \sin \omega t -\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.三角関数の和積の公式」より,上式を整理すると,
\[
\begin{eqnarray}
v_{\mathrm {uvf}}\left( \omega t \right) &=&\frac {2E_{\mathrm {d}}}{\pi }\left\{ \sin \omega t -\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \\[ 5pt ]
&=&\frac {2E_{\mathrm {d}}}{\pi }\left[ 2\cos \left\{ \frac {\displaystyle \omega t +\left( \omega t-\frac {2}{3}\pi \right) }{2}\right\}\sin \left\{ \frac {\displaystyle \omega t -\left( \omega t-\frac {2}{3}\pi \right) }{2}\right\} \right] \\[ 5pt ]
&=&\frac {2E_{\mathrm {d}}}{\pi }\left\{ 2\cos \left( \omega t-\frac {\pi }{3} \right) \sin \frac {\pi }{3} \right\} \\[ 5pt ]
&=&\frac {2E_{\mathrm {d}}}{\pi }\times 2\times \frac {\sqrt {3}}{2}\cos \left( \omega t-\frac {\pi }{3} \right) \\[ 5pt ]
&=&\frac {2\sqrt {3}E_{\mathrm {d}}}{\pi }\cos \left( \omega t-\frac {\pi }{3} \right) \\[ 5pt ]
&=&\frac {2\sqrt {3}E_{\mathrm {d}}}{\pi }\sin \left( \omega t+\frac {\pi }{6} \right) (∵\cos \theta = \sin \left( \theta +\frac {\pi }{2}\right) ) \\[ 5pt ]
\end{eqnarray}
\]
と求められ,その実効値\( \ V_{\mathrm {uvf}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {uvf}} &=&\frac {1}{\sqrt {2}}\cdot \frac {2\sqrt {3}E_{\mathrm {d}}}{\pi } \\[ 5pt ]
&=&\frac {\sqrt {6}E_{\mathrm {d}}}{\pi } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ E_{\mathrm {d}} \ \)の\( \ \displaystyle \frac {\sqrt {6}}{\pi } \ \)倍と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは