《機械・制御》〈変圧器〉[H25:問2]単相変圧器のV結線に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

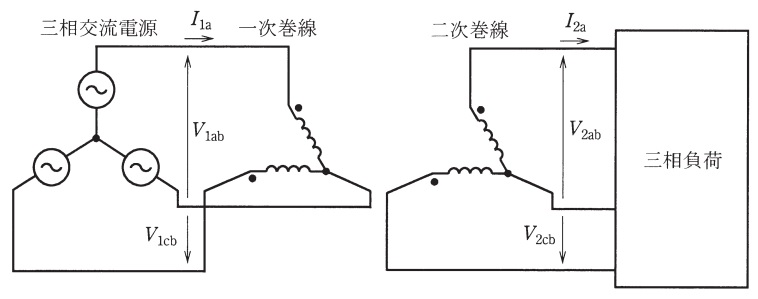
図のように同一の単相変圧器$\ 2 \ $台を$\ \mathrm {V} \ $結線し，一次側を線間電圧$\ 400 \ \mathrm {[V]} \ $の平衡三相交流電源に接続する。一次巻線と二次巻線の巻数比は$\ 2：1 \ $であり，一次及び二次の漏れリアクタンスはそれぞれ$\ 0.32 \ \mathrm {[\Omega ]} \ $，$\ 0.12 \ \mathrm {[\Omega ]} \ $である。ある三相負荷を二次側に接続すると，三相交流電源には$\ 50 \ \mathrm {[A]} \ $で力率$\ 1 \ $の平衡三相電流が流れた。次の問に答えよ。ただし，励磁電流，鉄損及び巻線抵抗は無視でき，変圧器鉄心は磁気飽和しないものとする。

(1)　無負荷時の二次電圧$\ V_{\mathrm {2ab}} \ \mathrm {[V]} \ $を求めよ。

(2)　三相負荷を接続した場合の変圧器二次電流$\ I_{\mathrm {2a}} \ \mathrm {[A]} \ $を求めよ。

(3)　一次及び二次の漏れリアクタンスを合成したリアクタンスの二次側換算値$\ \mathrm {[\Omega ]} \ $を求めよ。

(4)　負荷接続時の変圧器二次電圧$\ V_{\mathrm {2ab}} \ \mathrm {[V]} \ $及び$\ V_{\mathrm {2cb}} \ \mathrm {[V]} \ $を求めよ。

(5)　$\ 2 \ $台の変圧器がそれぞれ負荷に供給する電力$\ \mathrm {[kW]} \ $を求めよ。

【ワンポイント解説】

(1)～(3)が易しく，(4)→(5)になるにつれて徐々に難易度が上がっていく問題となっています。配点は公表されていませんが、おそらく均等であると思われるので，(1)～(3)を落とさない様に注意が必要です。

1.変圧器の一次側，二次側換算
変圧比$\ a \ $の変圧器があった場合，一次側，二次側換算は以下の通りとなります。
$$\begin{array}{|c|c|c|} \hline & 一次側→二次側換算値 & 二次側→一次側換算値 \\ \hline 電圧 \ V \ & \displaystyle \frac {1}{a}V & aV \\ \hline 電流 \ I \ & aI & \displaystyle \frac {1}{a}I \\ \hline 抵抗 \ R \ & \displaystyle \frac {1}{a^{2}}R & a^{2}R \\ \hline リアクタンス \ X \ & \displaystyle \frac {1}{a^{2}}X & a^{2}X \\ \hline \end{array}$$

【解答】

(1)無負荷時の二次電圧$\ V_{\mathrm {2ab}} \ \mathrm {[V]} \ $
ワンポイント解説「1.変圧器の一次側，二次側換算」の通り，無負荷時の二次電圧$\ V_{\mathrm {2ab}} \ $は，
$$\begin{eqnarray} V_{\mathrm {2ab}}&=&V_{\mathrm {1ab}}\times \frac {1}{a} \\[ 5pt ] &=&400\times \frac {1}{2} \\[ 5pt ] &=&200 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(2)三相負荷を接続した場合の変圧器二次電流$\ I_{\mathrm {2a}} \ \mathrm {[A]} \ $
ワンポイント解説「1.変圧器の一次側，二次側換算」の通り，三相負荷を接続した場合の変圧器二次電流$\ I_{\mathrm {2a}} \ $は，
$$\begin{eqnarray} I_{\mathrm {2a}}&=&I_{\mathrm {1a}}\times a \\[ 5pt ] &=&50\times 2 \\[ 5pt ] &=&100 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(3)一次及び二次の漏れリアクタンスを合成したリアクタンスの二次側換算値$\ \mathrm {[\Omega ]} \ $
ワンポイント解説「1.変圧器の一次側，二次側換算」の通り，一次漏れリアクタンスの二次側換算値$\ x_{1}^{\prime } \ $は，
$$\begin{eqnarray} x_{1}^{\prime }&=&x_{1}\times \frac {1}{a^{2}} \\[ 5pt ] &=&0.32\times \frac {1}{2^{2}} \\[ 5pt ] &=&0.08 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}$$ となる。よって，一次及び二次の漏れリアクタンスを合成したリアクタンスの二次側換算値$\ x_{1}^{\prime }+x_{2} \ $は，
$$\begin{eqnarray} x_{1}^{\prime }+x_{2}&=&0.08+0.12 \\[ 5pt ] &=&0.20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(4)負荷接続時の変圧器二次電圧$\ V_{\mathrm {2ab}} \ \mathrm {[V]} \ $及び$\ V_{\mathrm {2cb}} \ \mathrm {[V]} \ $
題意より，一次電圧の二次換算電圧を$\ V_{\mathrm {1ab}}^{\prime }=200 \ \mathrm {[V]} \ $として，二次側換算の一相分等価回路は図1のようになる。

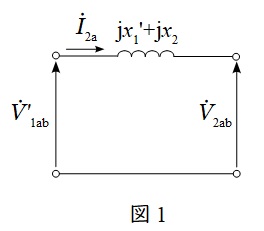
図1より，$\ {\dot V}_{\mathrm {1ab}}^{\prime } \ $を基準にベクトル図を描くと，$\ {\dot I}_{\mathrm {2a}} \ $は$\ {\dot V}_{\mathrm {1ab}}^{\prime } \ $より$\ \displaystyle \frac {\pi }{6} \ $遅れているので，図2のようになる。図2より，$\ {\dot I}_{\mathrm {2a}} \ $の大きさは，
$$\begin{eqnarray} {\dot I}_{\mathrm {2a}}&=&100\left( \displaystyle \cos \frac {\pi }{6}-\mathrm {j}\sin \frac {\pi }{6}\right) \\[ 5pt ] &=&50\sqrt {3}-\mathrm {j}50 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ であるから，$\ {\dot V}_{\mathrm {2ab}} \ $は，
$$\begin{eqnarray} {\dot V}_{\mathrm {2ab}}&=&{\dot V}_{\mathrm {1ab}}^{\prime }-\mathrm {j}\left( x_{1}^{\prime }+x_{2}\right) {\dot I}_{\mathrm {2a}} \\[ 5pt ] &=&200-\mathrm {j}0.20\times \left( 50\sqrt {3}-\mathrm {j}50\right) \\[ 5pt ] &=&190-\mathrm {j}10\sqrt {3} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ となるので，その大きさは，
$$\begin{eqnarray} V_{\mathrm {2ab}}&=&\sqrt {190^{2}+\left( 10\sqrt {3}\right) ^{2}} \\[ 5pt ] &≒&190.79　→　191 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

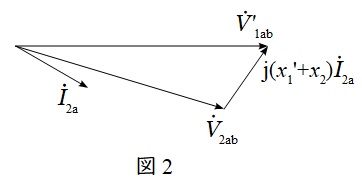
同様に$\ {\dot V}_{\mathrm {1ab}}^{\prime } \ $を基準に$\ {\dot V}_{\mathrm {2cb}} \ $のベクトル図を描くと，図3のようになる。図3より，$\ {\dot I}_{\mathrm {2c}} \ $の大きさは，
$$\begin{eqnarray} {\dot I}_{\mathrm {2c}}&=&100\left( \displaystyle \cos \frac {\pi }{2}+\mathrm {j}\sin \frac {\pi }{2}\right) \\[ 5pt ] &=&\mathrm {j}100 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ であり，$\ {\dot V}_{\mathrm {1cb}}^{\prime } \ $の大きさは，
$$\begin{eqnarray} {\dot V}_{\mathrm {1cb}}^{\prime }&=&-{\dot V}_{\mathrm {1bc}}^{\prime } \\[ 5pt ] &=&-\left( -100-\mathrm {j}100\sqrt {3}\right) \\[ 5pt ] &=&100+\mathrm {j}100\sqrt {3} \\[ 5pt ] \end{eqnarray}$$ であるから，$\ {\dot V}_{\mathrm {2cb}} \ $は，
$$\begin{eqnarray} {\dot V}_{\mathrm {2cb}}&=&{\dot V}_{\mathrm {1cb}}^{\prime }-\mathrm {j}\left( x_{1}^{\prime }+x_{2}\right) {\dot I}_{\mathrm {2c}} \\[ 5pt ] &=&100+\mathrm {j}100\sqrt {3}-\mathrm {j}0.20\times \mathrm {j}100 \\[ 5pt ] &=&120+\mathrm {j}100\sqrt {3} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ となり，その大きさは，
$$\begin{eqnarray} V_{\mathrm {2cb}}&=&\sqrt {120^{2}+\left( 100\sqrt {3}\right) ^{2}} \\[ 5pt ] &≒&210.71　→　211 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(5)$\ 2 \ $台の変圧器がそれぞれ負荷に供給する電力$\ \mathrm {[kW]} \ $
遅れ無効電力を正として，それぞれが負荷に供給する電力を求めると，
$$\begin{eqnarray} \mathrm {Re}\left[ {\dot V}_{\mathrm {2ab}}\overline {\dot I}_{\mathrm {2a}}\right] &=&\mathrm {Re}\left[ \left( 190-\mathrm {j}10\sqrt {3}\right) \left( 50\sqrt {3}+\mathrm {j}50\right) \right] \\[ 5pt ] &=&\mathrm {Re}\left[ 10000\sqrt {3}+\mathrm {j}8000 \right] \\[ 5pt ] &≒&17300 \ \mathrm {[W]}　→　17.3 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}$$ $$\begin{eqnarray} \mathrm {Re}\left[ {\dot V}_{\mathrm {2cb}}\overline {\dot I}_{\mathrm {2c}}\right] &=&\mathrm {Re}\left[ \left( 120+\mathrm {j}100\sqrt {3}\right) \left( -\mathrm {j}100\right) \right] \\[ 5pt ] &=&\mathrm {Re}\left[ 10000\sqrt {3}-\mathrm {j}12000 \right] \\[ 5pt ] &≒&17300 \ \mathrm {[W]}　→　17.3 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

※　試験センターでは一次入力から電力を求める方法を別解としておりますが，これぐらいの計算であったら普通に計算すれば良いと思います。