Contents
【問題】
【難易度】★★★☆☆(普通)
図のように,電圧線及び中性線の各部の抵抗が\( \ 0.2 \ \mathrm {\Omega } \ \)の単相\(3\)線式低圧配電線路において,末端の\( \ \mathrm {AC} \ \)間に太陽光発電設備が接続されている。各部の電圧及び電流が図に示された値であるとき,次の(a)及び(b)の問に答えよ。ただし,負荷は定電流特性で力率は\( \ 1 \ \),太陽光発電設備の出力(交流)は電流\( \ I \ \mathrm {[A]} \ \),力率\( \ 1 \ \)で一定とする。また,線路のインピーダンスは抵抗とし,図示していないインピーダンスは無視するものとする。
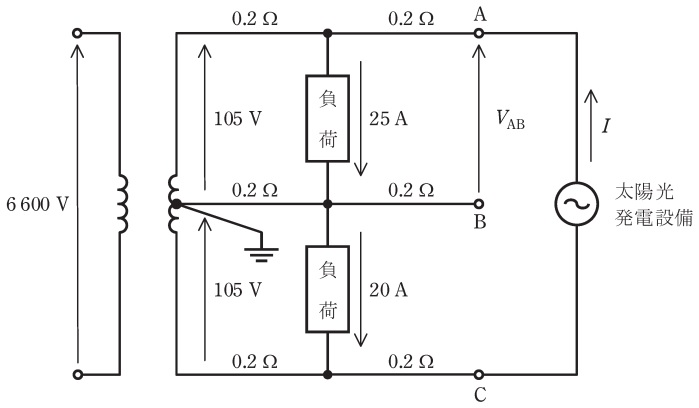
(a) 太陽光発電設備を接続する前の\( \ \mathrm {AB} \ \)間の端子電圧\( \ V_{\mathrm {AB}} \ \)の値\( \ \mathrm {[V]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(96\) (2) \(99\) (3) \(100\) (4) \(101\) (5) \(104\)
(b) 太陽光発電設備を接続したところ,\( \ \mathrm {AB} \ \)間の端子電圧\( \ V_{\mathrm {AB}} \ \mathrm {[V]} \ \)が\( \ 107 \ \mathrm {V} \ \)となった。このときの太陽光発電設備の出力電流(交流)\( \ I \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(5\) (2) \(15\) (3) \(20\) (4) \(25\) (5) \(30\)
【ワンポイント解説】
問題文や回路図を見るとやや複雑な問題に見えるかもしれませんが,整理して考えると電気回路の問題の延長であることに気付くと思います。こういう問題ではできるだけ図に落とし込んで,時間があれば回路図を自分で描くと間違いが減ると思いますので,ぜひ取り組んでみて下さい。
【解答】
(a)解答:(2)
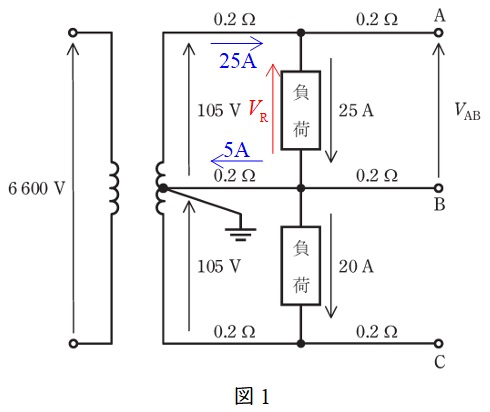
太陽光発電設備接続前の回路図を描くと図1のようになる。変圧器の中性線を流れる電流は各負荷を流れる電流の差\( \ 25-20=5 \ \mathrm {A} \ \)であるから,キルヒホッフの法則より,
\[
\begin{eqnarray}
105&=&0.2 \times 25 + V_{\mathrm {R}} + 0.2 \times 5 \\[ 5pt ]
105&=&5 + V_{\mathrm {R}} + 1 \\[ 5pt ]
V_{\mathrm {R}}&=&99 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\(\mathrm {A}\)点及び\(\mathrm {B}\)点には電流は流れないので,\(V_{\mathrm {AB}}=V_{\mathrm {R}}\)となり,\(V_{\mathrm {AB}}=99 \ \mathrm {V}\)となる。
(b)解答:(3)
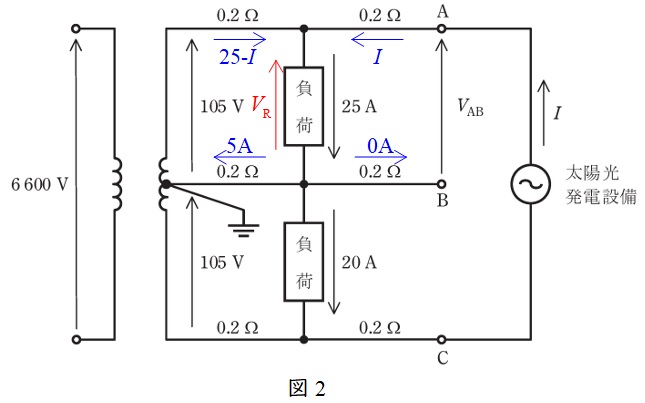
太陽光発電設備接続後の回路図を描くと図2のようになる。太陽光発電設備から供給される電流が\( \ I \ \mathrm {[A]} \ \)であるので,変圧器側から供給される電流は\( \ 25-I \ \mathrm {[A]} \ \)となる。
(a)と同様にキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
105&=&0.2 \times \left( 25 -I \right) + V_{\mathrm {R}} + 0.2 \times 5 \\[ 5pt ]
105&=&5 -0.2I + V_{\mathrm {R}} + 1 \\[ 5pt ]
V_{\mathrm {R}}&=&99+0.2I \ \mathrm {[V]}
\end{eqnarray}
\]
となる。一方,\( \ \mathrm {AB} \ \)間の端子電圧\( \ V_{\mathrm {AB}} \ \mathrm {[V]} \ \)が\( \ 107 \ \mathrm {V} \ \)であるから,
\[
\begin{eqnarray}
107&=&0.2 I + V_{\mathrm {R}} \\[ 5pt ]
107&=&0.2 I +99+0.2I \\[ 5pt ]
I&=&20 \ \mathrm {[A]}
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは