《法規》〈電気設備技術基準〉[H21:問12]支持物に設ける支線の張力と必要条数に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

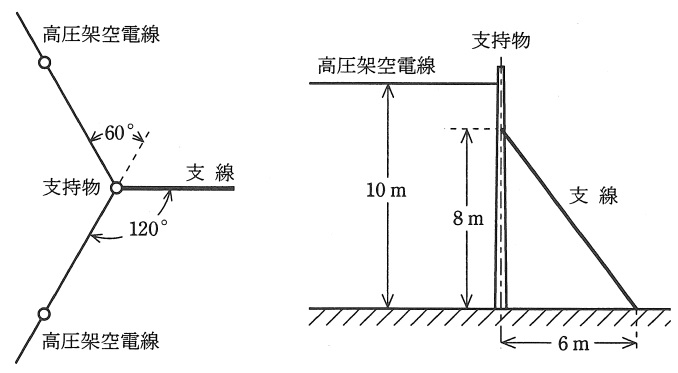
図のように，高圧架空電線路中で水平角度が\( \ 60 \ \mathrm {[°]} \ \)の電線路となる部分の支持物（\( \ \mathrm {A} \ \)種鉄筋コンクリート柱）に下記の条件で電気設備技術基準の解釈に適合する支線を設けるものとする。

(ア)　高圧架空電線の取り付け高さを\( \ 10 \ \mathrm {[m]} \ \)，支線の支持物への取り付け高さを\( \ 8 \ \mathrm {[m]} \ \)，この支持物の地表面の中心点と支線の地表面までの距離を\( \ 6 \ \mathrm {[m]} \ \)とする。

(イ)　高圧架空電線と支線の水平角度を\( \ 120 \ \mathrm {[°]} \ \)，高圧架空電線の想定最大水平張力を\( \ 9.8 \ \mathrm {[kN]} \ \)とする。

(ウ)　支線には亜鉛めっき鋼より線を用いる。その素線は，直径\( \ 2.6 \ \mathrm {[mm]} \ \)，引張強さ\( \ 1.23 \ \mathrm {[kN / {mm}^{2}]} \ \)である。素線のより合わせによる引張荷重の減少係数を\( \ 0.92 \ \)とし，支線の安全率を\( \ 1.5 \ \)とする。

このとき，次の(a)及び(b)に答えよ。

(a)　支線に働く想定最大荷重\( \ \mathrm {[kN]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 10.2 \ \)　　(2)　\( \ 12.3 \ \)　　(3)　\( \ 20.4 \ \)　　(4)　\( \ 24.5 \ \)　　(5)　\( \ 40.1 \ \)

(b)　支線の素線の最少の条数として，正しいのは次のうちどれか。

　(1)　\( \ 3 \ \)　　(2)　\( \ 7 \ \)　　(3)　\( \ 9 \ \)　　(4)　\( \ 13 \ \)　　(5)　\( \ 19 \ \)

【ワンポイント解説】

\( \ 2 \ \)本の電線が接続されている支持物に設ける支線の張力と必要条数を求める問題です。
電気設備技術基準からの出題ですが，内容は物理の力学を理解しているかを問う問題です。
ぜひ内容を理解して得点源とできるようにしましょう。

1.支線の張力
①支線と電線の取付高さが同じ場合
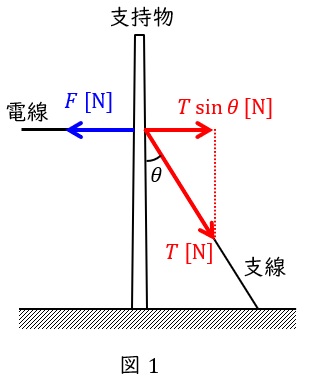
図1のように，電線の張力が\( \ F \ \mathrm {[N]} \ \)，支線の張力が\( \ T \ \mathrm {[N]} \ \)，支持物と支線のなす角が\( \ \theta \ \mathrm {[rad]} \ \)であるとすると，支持物に加わる水平張力が等しくなければならないから，
\[
\begin{eqnarray}
F&=&T\sin \theta \\[ 5pt ] T&=&\frac {F}{\sin \theta } \\[ 5pt ] \end{eqnarray}
\] となります。

②支線と電線の取付高さが異なる場合
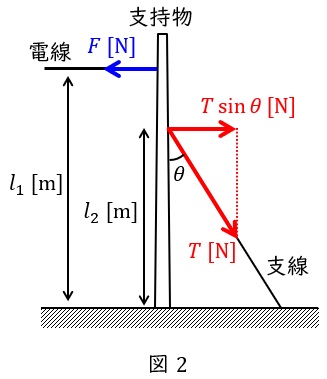
図2のように，電線の張力が\( \ F \ \mathrm {[N]} \ \)で取付高さが\( \ l_{1} \ \mathrm {[m]} \ \)，支線の張力が\( \ T \ \mathrm {[N]} \ \)で取付高さが\( \ l_{2} \ \mathrm {[m]} \ \)，支持物と支線のなす角が\( \ \theta \ \mathrm {[rad]} \ \)であるとすると，支持物に加わる力のモーメントが等しくなければならないから，
\[
\begin{eqnarray}
Fl_{1}&=&T\sin \theta \cdot l_{2} \\[ 5pt ] T&=&\frac {F}{\sin \theta }\cdot \frac {l_{1}}{l_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.電線の許容引張荷重
電気設備の技術基準の解釈第66条において，許容引張荷重は電線の引張強さから安全率を加味して選定するように規定されていて，
\[
\begin{eqnarray}
許容引張荷重 &=&\frac {電線の引張強さ}{安全率} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(a)解答：(3)
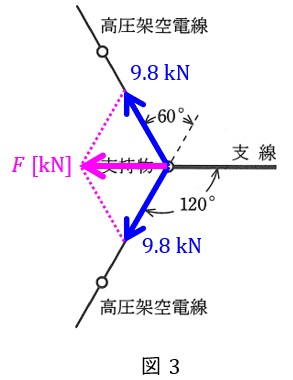
まず高圧架空電線の合成想定最大張力\( \ F \ \mathrm {[kN]} \ \)を考えると，図3の通り，高圧架空電線同士の水平角度が\( \ 120 \ \mathrm {[°]} \ \)なので，それぞれと水平角度が\( \ 60 \ \mathrm {[°]} \ \)の方向に合成想定最大張力\( \ F \ \mathrm {[kN]} \ \)が加わる。したがって，
\[
\begin{eqnarray}
F&=&9.8 \ \mathrm {[kN]} \\[ 5pt ] \end{eqnarray}
\] となる。

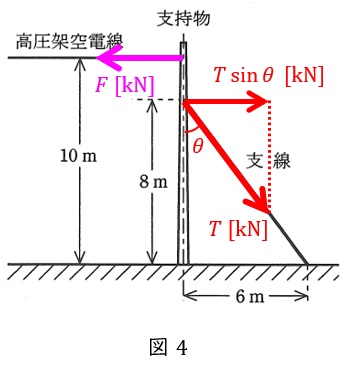
次に，合成想定最大張力\( \ F=9.8 \ \mathrm {[kN]} \ \)と釣り合う支線の張力\( \ T \ \mathrm {[kN]} \ \)とすると，各張力の関係は図4の通りとなる。支線と支持物のなす角を\( \ \theta \ \mathrm {[rad]} \ \)とすれば，
\[
\begin{eqnarray}
\sin \theta &=&\frac {6}{\sqrt {6^{2}+8^{2}}} \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] となるので，力のモーメントが等しいことから，ワンポイント解説「1.支線の張力」の通り，
\[
\begin{eqnarray}
F\times 10&=&T\sin \theta \times 8 \\[ 5pt ] 9.8 \times 10&=&T\times 0.6 \times 8 \\[ 5pt ] T&=&\frac {9.8 \times 10}{0.6 \times 8 } \\[ 5pt ] &≒&20.42　→　20.4 \ \mathrm {[kN]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
素線\( \ 1 \ \)本あたりの引張荷重\( \ T_{\mathrm {1}} \ \mathrm {[kN]} \ \)は，素線の直径\( \ 2.6 \ \mathrm {[mm]} \ \)，引張強さ\( \ 1.23 \ \mathrm {[kN / {mm}^{2}]} \ \)より，
\[
\begin{eqnarray}
T_{\mathrm {1}}&=&\pi \left( \frac {2.6}{2} \right) ^{2}\times 1.23 \\[ 5pt ] &≒&6.530 \ \mathrm {[kN]} \\[ 5pt ] \end{eqnarray}
\] なる。より合わせる支線の条数を\( \ n \ \)とすると，引張荷重の減少係数が\( \ 0.92 \ \)，支線の安全率が\( \ 1.5 \ \)であるから，
\[
\begin{eqnarray}
1.5T&＜&T_{\mathrm {1}}n\times 0.92 \\[ 5pt ] 1.5\times 20.42&＜&6.530\times n\times 0.92 \\[ 5pt ] n&＞&\frac {1.5\times 20.42}{6.530\times 0.92} \\[ 5pt ] n&＞&5.10 \\[ 5pt ] \end{eqnarray}
\] となり，支線は\( \ 6 \ \)条以上必要となるので，選択肢としては最も近い\( \ 7 \ \)条が正答となる。