《法規》〈電気施設管理〉[H21:問9]工場等における電気設備の運用管理に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，工場等における電気設備の運用管理に関する記述である。

電気機器は適正な電圧で使用することにより，効率的な運用を図ることができる。このため電気管理者にとって，\( \ \fbox {　 （ア） 　} \ \)の検討を行うことは重要である。

また，電力損失の抑制対策として，次のように幾つかの例が挙げられる。

①　電気機器と並列にコンデンサ設備を設置し，\( \ \fbox {　 （イ） 　} \ \)をすることにより電力損失の低減を図る。

②　変圧器は，適正な\( \ \fbox {　 （ウ） 　} \ \)を維持するように，機器の稼働台数の調整及び負荷の適正配分を行う。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる語句として，正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　短路保護協調　 & 　力率改善　 & 　需要率　 \\
\hline
(2) & 　電圧降下　　　 & 　電圧維持　 & 　負荷率　 \\
\hline
(3) & 　地絡保護協調　 & 　力率改善　 & 　不等率　 \\
\hline
(4) & 　電圧降下　　　 & 　力率改善　 & 　需要率　 \\
\hline
(5) & 　短路保護協調　 & 　電圧維持　 & 　需要率　 \\
\hline
\end{array}
\]

【ワンポイント解説】

工場等の需要家内における電圧の維持と電力損失の抑制対策に関する問題です。
並列にコンデンサを設置することや変圧器の適正台数の運用等は電力科目や法規科目の電気施設管理にもよく出題される内容です。同じ年度の平成21年電力科目問17でも出題されていますので，学習してみて下さい。

1.送電線の送電電力と電力損失
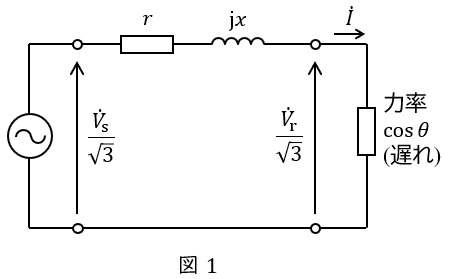
送電端の電圧が\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)，受電端の電圧が\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \)，送電線の\( \ 1 \ \)線あたりの抵抗が\( \ r \ \mathrm {[\Omega ]} \ \)，リアクタンスが\( \ x \ \mathrm {[\Omega ]} \ \)，送電線に流れる電流が\( \ I \ \mathrm {[A]} \ \)，負荷の力率が\( \ \cos \theta \ \)であるとすると，送電線の一相分等価回路は図1のように描くことができます。

このとき，負荷電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&\sqrt {3}V_{\mathrm {r}}I\cos \theta \\[ 5pt ] \end{eqnarray}
\] となり，上式より，
\[
\begin{eqnarray}
I &=&\frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta } \\[ 5pt ] \end{eqnarray}
\] であるため，送電線での電力損失\( \ P_{\mathrm {L}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {L}} &=&3rI^{2} \\[ 5pt ] &=&3r\left( \frac {P}{\sqrt {3}V_{\mathrm {r}}\cos \theta }\right) ^{2} \\[ 5pt ] &=&\frac {P^{2}r}{V_{\mathrm {r}}^{2}\cos ^{2}\theta } \\[ 5pt ] \end{eqnarray}
\] となります。

2.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(4)
(ア)
電気機器の電圧を適正な範囲に維持するためには，電圧降下の検討を行うことが重要です。三相線路における電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)の近似式は，
\[
\begin{eqnarray}
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] で求められ，力率\( \ \cos \theta \ \)を調整する等により改善することが可能です。

(イ)
ワンポイント解説「1.送電線の送電電力と電力損失」の通り，電力損失は力率\( \ \cos \theta \ \)の\( \ 2 \ \)乗に反比例するので，力率改善をすることにより電力損失の低減をすることができます。

(ウ)
ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，機器の稼働台数（設備容量）は需要率に関連する内容となります。