《法規》〈電気施設管理〉[R3:問13]需要家の需要率，不等率，負荷率に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

需要家\( \ \mathrm {A} \ \)～\( \ \mathrm {C} \ \)にのみ電力を供給している変電所がある。

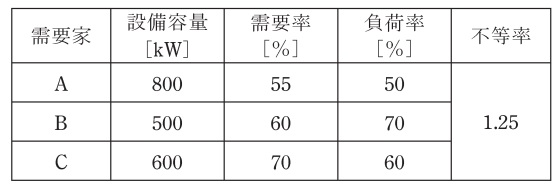
各需要家の設備容量と，ある\( \ \mathrm {1} \ \)日（\( \ \mathrm {0} \ \)～\( \ \mathrm {24} \ \)時）の需要率，負荷率及び需要家\( \ \mathrm {A} \ \)～\( \ \mathrm {C} \ \)の不等率を表に示す値とする。表の記載に基づき，次の(a)及び(b)の問に答えよ。

(a)　\( \ \mathrm {3} \ \)需要家\( \ \mathrm {A} \ \)～\( \ \mathrm {C} \ \)の\( \ \mathrm {1} \ \)日の需要電力量を合計した総需要電力量の値\( \ \mathrm {[kW\cdot h]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 10 \ 480 \ \)　　(2)　\( \ 16 \ 370 \ \)　　(3)　\( \ 20 \ 460 \ \)　　(4)　\( \ 26 \ 650 \ \)　　(5)　\( \ 27 \ 840 \ \)

(b)　変電所から見た総合負荷率の値\( \ \mathrm {[％]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，送電損失，需要家受電設備損失は無視するものとする。

　(1)　\( \ 42 \ \)　　(2)　\( \ 59 \ \)　　(3)　\( \ 62 \ \)　　(4)　\( \ 73 \ \)　　(5)　\( \ 80 \ \)

【ワンポイント解説】

需要率，不等率，負荷率を使用した計算問題です。
いずれの公式も試験本番になると「あれ？」となる公式です。出題頻度も比較的高い分野となるので，試験直前に必ず復習し本番を迎えるようにしましょう。

1.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(2)
ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，\( \ \displaystyle 需要率=\frac {最大需要電力}{設備容量}\times 100　[％] \ \)であるから，各需要家の最大需要電力\( \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
{最大需要電力}_{\mathrm {A}}&=&\frac {設備容量_{\mathrm {A}}\times 需要率_{\mathrm {A}}}{100} \\[ 5pt ] &=&\frac {800\times 55}{100} \\[ 5pt ] &=&440 \ \mathrm {[kW]} \\[ 5pt ] {最大需要電力}_{\mathrm {B}}&=&\frac {設備容量_{\mathrm {B}}\times 需要率_{\mathrm {B}}}{100} \\[ 5pt ] &=&\frac {500\times 60}{100} \\[ 5pt ] &=&300 \ \mathrm {[kW]} \\[ 5pt ] {最大需要電力}_{\mathrm {C}}&=&\frac {設備容量_{\mathrm {C}}\times 需要率_{\mathrm {C}}}{100} \\[ 5pt ] &=&\frac {600\times 70}{100} \\[ 5pt ] &=&420 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ \displaystyle 負荷率=\frac {平均需要電力}{最大需要電力}\times 100　[％] \ \)であるから，各需要家の平均需要電力\( \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
{平均需要電力}_{\mathrm {A}}&=&\frac {最大需要電力_{\mathrm {A}}\times 負荷率_{\mathrm {A}}}{100} \\[ 5pt ] &=&\frac {440\times 50}{100} \\[ 5pt ] &=&220 \ \mathrm {[kW]} \\[ 5pt ] {平均需要電力}_{\mathrm {B}}&=&\frac {最大需要電力_{\mathrm {B}}\times 負荷率_{\mathrm {B}}}{100} \\[ 5pt ] &=&\frac {300\times 70}{100} \\[ 5pt ] &=&210 \ \mathrm {[kW]} \\[ 5pt ] {平均需要電力}_{\mathrm {C}}&=&\frac {最大需要電力_{\mathrm {C}}\times 負荷率_{\mathrm {C}}}{100} \\[ 5pt ] &=&\frac {420\times 60}{100} \\[ 5pt ] &=&252 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，全需要家の需要電力量の合計\( \ \mathrm {[kW\cdot h]} \ \)は，
\[
\begin{eqnarray}
{総需要電力量}&=&\left( {平均需要電力}_{\mathrm {A}}+{平均需要電力}_{\mathrm {B}}+{平均需要電力}_{\mathrm {C}}\right) \times 24 \\[ 5pt ] &=&\left( 220+210+252\right) \times 24 \\[ 5pt ] &=&16 \ 368　→　16 \ 370 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
ワンポイント解説「1.需要率，不等率，負荷率の定義」の通り，\( \ \displaystyle 不等率=\frac {個々の最大需要電力の合計}{合成の最大需要電力} \ \)であるから，需要家の合成最大需要電力\( \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
{合成最大需要電力}&=&\frac {個々の最大需要電力の合計}{不等率} \\[ 5pt ] &=&\frac {440+300+420}{1.25} \\[ 5pt ] &=&928 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，総合負荷率\( \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
総合負荷率&=&\frac {全体の平均需要電力}{合成最大需要電力}\times 100 \\[ 5pt ] &=&\frac {220+210+252}{928}\times 100 \\[ 5pt ] &≒&73.49　→　73 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。