《機械》〈変圧器〉[H21:問7] Y-Δ 結線した変圧器の変圧比の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

同一仕様である\( \ 3 \ \)台の単相変圧器の一次側を星形結線，二次側を三角結線にして，三相変圧器として使用する。\( \ 20 \ \mathrm {[\Omega ]} \ \)の抵抗器\( \ 3 \ \)個を星形に接続し，二次側に負荷として接続した。一次側を\( \ 3 \ 300 \ \mathrm {[V]} \ \)の三相高圧母線に接続したところ，二次側の負荷電流は\( \ 12.7 \ \mathrm {[A]} \ \)であった。この単相変圧器の変圧比として，最も近いのは次のうちどれか。

ただし，変圧器の励磁電流，インピーダンス及び損失は無視するものとする。

　(1)　\( \ 4.33 \ \)　　(2)　\( \ 7.50 \ \)　　(3)　\( \ 13.0 \ \)　　(4)　\( \ 22.5 \ \)　　(5)　\( \ 39.0 \ \)

【ワンポイント解説】

\( \ \mathrm {Y-\Delta } \ \)結線した変圧器の一次，二次の各パラメータから変圧比を求める問題です。
相電圧と線間電圧の関係をしっかりと理解できているかが問われている問題で，誤りの選択肢もミスをすると選択してしまうように作られています。
図が与えられていないので，問題を整理するために図を描いて解くことをお勧めします。

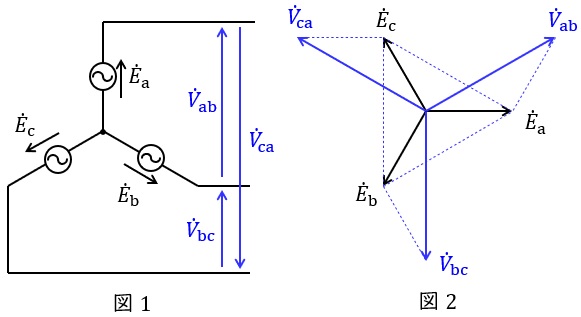
1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図1のような三相対称電源がある時，線間電圧と相電圧の関係は図2のベクトル図のようになり，線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ] V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ] V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)進みであることが分かります。

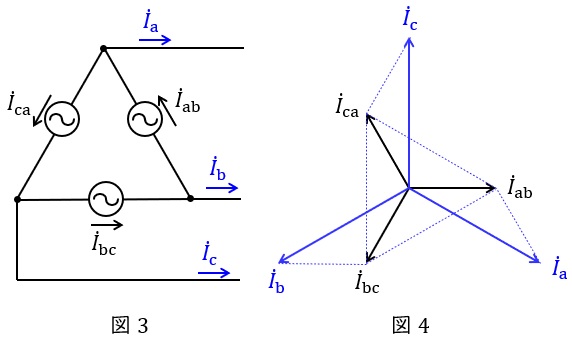
2.\( \ \Delta \ \)結線における相電流と線電流の関係
図3のような三相対称電源がある時，線電流と相電流の関係は図4のベクトル図のようになり，線電流の大きさは相電流の大きさと比較すると，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ] I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ] I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)遅れであることが分かります。

【解答】

解答：(1)
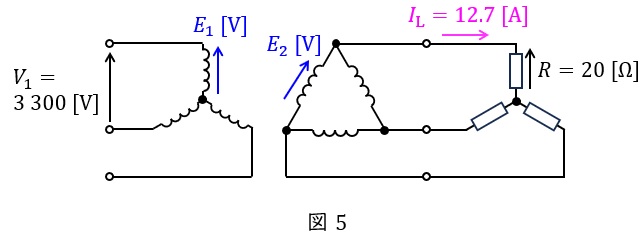
単相変圧器の一次電圧を\( \ E_{1} \ \mathrm {[V]} \ \)，二次電圧を\( \ E_{2} \ \mathrm {[V]} \ \)として，題意に沿って図を描くと図5のようになる。
図5より，変圧器の一次電圧\( \ E_{1} \ \mathrm {[V]} \ \)の大きさは，ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，
\[
\begin{eqnarray}
E_{\mathrm {1}} &=&\frac {V_{1}}{\sqrt {3}} \\[ 5pt ] &=&\frac {3 \ 300}{\sqrt {3}} \\[ 5pt ] &≒&1 \ 905 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。一方，負荷電圧\( \ E_{\mathrm {L}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {L}} &=&RI_{\mathrm {L}} \\[ 5pt ] &=&20\times 12.7 \\[ 5pt ] &=&254 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，変圧器の二次電圧\( \ E_{2} \ \mathrm {[V]} \ \)の大きさは，ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り，
\[
\begin{eqnarray}
E_{\mathrm {2}} &=&\sqrt {3}E_{\mathrm {L}} \\[ 5pt ] &=&\sqrt {3}\times 254 \\[ 5pt ] &≒&439.9 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，変圧器の変圧比\( \ a \ \)は，
\[
\begin{eqnarray}
a &=&\frac {E_{\mathrm {1}}}{E_{\mathrm {2}}} \\[ 5pt ] &=&\frac {1 \ 905}{439.9} \\[ 5pt ] &≒&4.33 \\[ 5pt ] \end{eqnarray}
\] と求められる。